Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 33

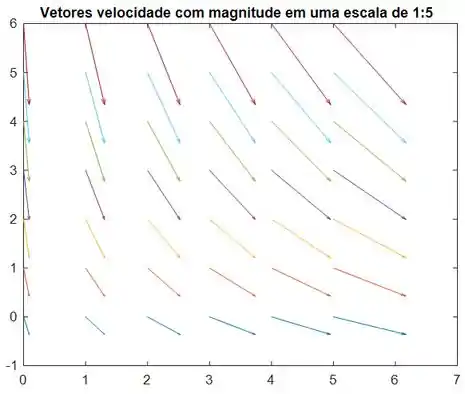
Considere o campo de velocidade em regime permanente, incompressível e bidimensional do Problema 4-32. Gere um gráfico vetorial de velocidade no quadrante superior direito de x = 0 a 5 e de y = 0 a 6 .

Passo 1

A questão pede que a gente desenhe um gráfico com os vetores velocidade V → de cada ponto do escoamento do Problema 4-32. A velocidade de cada partícula de fluido desse escoamento pode ser calculada pela equação abaixo.

V → = 0,5 + 1,2 ⋅ x ⏟ u i → + - 2,0 - 1,2 ⋅ y ⏟ v j →

onde u é a componente do eixo x da velocidade V → , v é a componente do eixo y da velocidade V → . Isso quer dizer que para esse escoamento bidimensional no plano x y :

u = 0,5 + 1,2 ⋅ x

v = - 2,0 - 1,2 ⋅ y

No próximo passo, vamos entender como usar essa informação para gerar o campo de velocidades no quadrante superior direito de x = 0 a 5 e de y = 0 a 6 .

Passo 2

Temos que transformar as equações de u e v nos vetores de velocidade V → de cada ponto do escoamento. Para isso, substituimos os valores das coordenadas de x e y do ponto nas equações de u e v . Por exemplo, como seria o vetor velocidade dos pontos 0,0 e 1,2 ? Para o ponto 0,0 , temos que x = 0 e y = 0 . Logo:

u = 0,5 + 1,2 ⋅ x       ⟹       u = 0,5 + 1,2 ⋅ 0       ⟹       u 0,0 = 0,5

v = - 2,0 - 1,2 ⋅ y     ⟹     v = - 2,0 - 1,2 ⋅ 0     ⟹       v 0,0 = - 2,0

Isso quer dizer que o vetor velocidade V → do ponto 0,0 tem a seguinte forma.

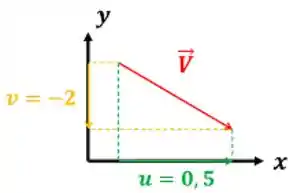
Para o ponto 1,2 , temos que x = 1 e y = 2 . Logo:

u = 0,5 + 1,2 ⋅ x       ⟹       u = 0,5 + 1,2 ⋅ 1       ⟹       u 1,2 = 1,7

v = - 2,0 - 1,2 ⋅ y     ⟹     v = - 2,0 - 1,2 ⋅ 2     ⟹       v 1,2 = - 4,4

Isso quer dizer que o vetor velocidade V → do ponto 1,2 tem a seguinte forma:

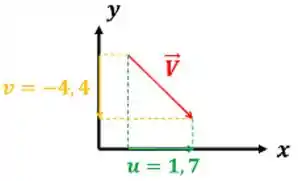
Passo 3

Desenhamos os vetores de dois pontos, mas a questão quer os vetores de mais pontos. O campo de velocidades do quadrante superior se encontra abaixo.

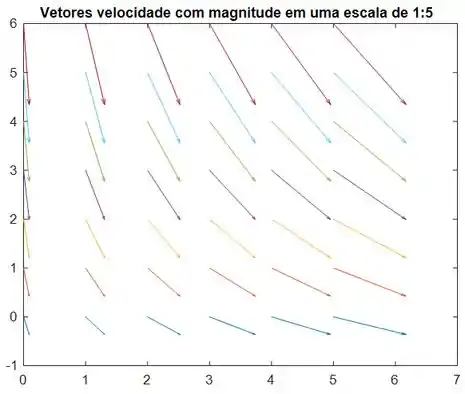
Esses vetores de velocidade estão em uma escala de 1 : 5 . Isso significa que as magnitudes dos vetores representados no gráfico são cinco vezes menores que as magnitudes reais.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Combine seus resultados do problema 4-80 para formar o tensor da taxa de deformação bidimensional ε i j no plano x y ε i j = ε x xε x y ε y x ε y y Os eixos x e y são principais?
Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40° C . Seja h = 1,6m m a altura da lacuna e d P / d x = - 230N / m 3 o gradiente de pressão.
Combine seus resultados do Problema 4 - 88 para formar o tensor taxa de deformação simétrico ϵ y . ϵ i j = ϵ r r ϵ r x ϵ x r ϵ x x Os eixos x e r são principais?
Considere o escoamento de Poiseuille bidimensional do problema 4-79. O fluido entre as placas é água a 40 ° C . Seja h = 1,6 m m a altura da lacuna e d P d x = - 230 N / m 3 o gradiente de pressão. Ca
Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40° C . Seja h = 1,6m m a altura da lacuna e d P / d x = - 230N / m 3 o gradiente de pressão.