Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 83

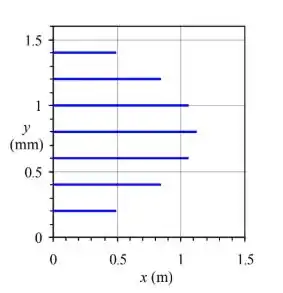
Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40   ° C . Seja h = 1,6   m m a altura da lacuna e d P / d x = - 230   N / m 3 o gradiente de pressão. Calcule e trace sete linhas de emissão geradas com uma varredura que introduz listras de tinta em x = 0 e y = 0,2 ,   0,4 ,   0,6 ,   0,8 ,   1,0 ,   1,2   e   1,4   m m . A tinta é introduzida de t = 0 a t = 10   s e as linhas de emissão devem ser traçadas em t = 10   s .

Passo 1

Fala aí galera, Bora pra mais uma questão de Mecânica dos Fluidos. Primeiramente, Como o fluxo é constante, as linhas, as linhas de fluxo são horizontais. Logo, nós precisamos integrar a componente de velocidade u em relação ao tempo durante o período especificado. O componente de velocidade horizontal é dada por:

u = 1 2 μ d P d x ( y 2 - h y )

Com isso, vamos obter a localização final x da primeira linha, temos:

x = x i n i c i o + ∫ t 0 t i u   d t = 0 + ∫ 0 10 1 2 μ d P d x y 2 - h y   d t x = 1 2 μ d P d x ( y 2 - h y ) ( 10   s )

Passo 2

Por fim, substituímos os valores fornecidos de y e os valores de μ e d P / d x na equação de localização final para calcular a posição final x de cada caminho. Traçando os caminhos, temos:

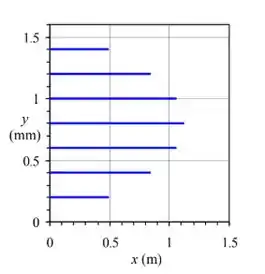
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma sonda fixa é colocada em um escoamento de fluido e mede a pressão e a temperatura como funções do tempo em determinado local do escoamento (Figura). Essa é umamedição lagrangiana ou euleriana? Exp
Considere o seguinte campo de velocidade em regime permanente e bidimensional: V → = u ,v = 0,5 + 1,2 x i → + ( - 2,0 - 1,2 y ) j → Existe algum ponto de estagnação nesse campo de escoamento? Se exist
Considere o seguinte campo de velocidade estacionário e bidimensional: V → = u ,v = a 2 - b - c x 2 i → + ( - 2 c b y + 2 c 2 x y ) j → Existe algum ponto de estagnação nesse campo de escoamento?Se ex
Considere o escoamento estacionário da água através do bocal de uma mangueira de jardim assimétrico . Ao longo do eixo central do bocal, a velocidade da água aumenta de u e n t r a d a para u s a í d
Cite e descreva brevemente os quatro tipos fundamentais de movimento ou deformação das partículas de fluido.