Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 86

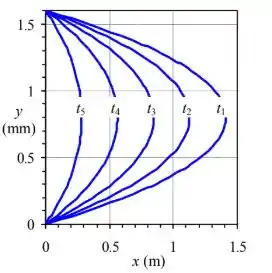
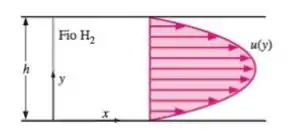
Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40   ° C . Seja h = 1,6   m m a altura da lacuna e d P / d x = - 230   N / m 3 o gradiente de pressão. Imagine um fio de bolha de hidrogênio esticado verticalmente através do canaç em x = 0 (Figura P 4 - 86 ) . O fio é pulsado, ligando e desligando, de forma que as bolhas são produzidas periodicamente para criar linhas de tempo. Cinco linhas de tempo distintas são geradas em t = 0 ,   2,5 ,     5,0 ,     7,5   e 10,0   s . Calcule e esboce a aparência dessas cinco linhas de tempo no instante t = 12,5   s .

Passo 1

Fala aí galera, Bora pra mais uma questão de Mecânica dos Fluidos. Primeiramente, como o fluxo é constante, as linhas de fluxo e as linhas de fluxo são todas linhas horizontais retas, mas as linhas de tempo são completamente diferentes de qualquer uma das outras. Para simular uma linha do tempo, integramos o componente de velocidade u em relação ao tempo no período especificado de t = 0 a t f = t f . Introduzimos as bolhas em x = 0 e em muitos valores de y (usamos 50 em nossa simulação). Ao conectar esses x locais a uma linha, simulamos uma linha do tempo. O componente de velocidade horizontal é dado por:

u = 1 2 μ d P d x ( y 2 - h y )

Integrando, temos:

x = x i n i c i o + ∫ t 0 t f u   d t = 0 + ∫ 0 t f 1 2 μ d P d x y 2 - h y   d t x = 1 2 μ d P d x y 2 - h y ( t f )                                  

Passo 2

Por fim, substituímos os valores de y   e os valores de μ e d P / d x na equação acima para calcular a posição x final de cada ponto na linha do tempo. Repetimos para os cinco valores de t f . Traçando as linhas, temos:

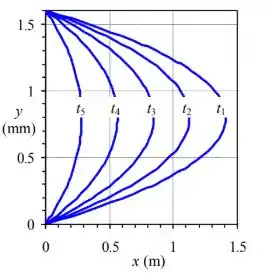
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a visualização do escoamento em uma asa-delta com abertura de 15° na Figura P4-27C. Estamos vendo linhas de corrente, linhas de emissão, linhas de trajetória ou linhas de tempo? Explique.Vis
Qual é a definição de uma linha de tempo? Como as linhas de tempo podem ser produzidas em um canal de água? Mencione uma aplicação na qual as linhas de tempo são mais úteis do que as linhas de emissão
Qual é a definição de uma linha de emissão? Como as linhas de emissão diferem das linhas de corrente?
Considere uma fatia transversal através de uma matriz de tubos de tocador de calor (Figura P4-31C). Para cada informação desejada, selecione o tipo de gráfico de visualização do escoamento (gráfico ve
Considere o seguinte campo de velocidade em regime permanente, incompressível e bidimensional: V → = u , v = 0,5 + 1,2 ⋅ x i → + - 2,0 - 1,2 ⋅ y j → Gere uma expressão analítica para as linhas de corr