Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 47a

Considere as cavidades formadas por um cone, um cilindro e uma esfera que têm o mesmo tamanho de abertura (d) e dimensão principal (L), como mostrado na figura.

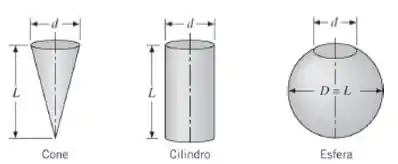
Determine o fator de forma entre a superfície interna de cada cavidade e sua abertura.

Passo 1

Vamos lá! A gente tem 3 cavidades diferentes e em todas elas existem uma abertura de diâmetro d e possuem dimensão L !!

A primeira coisa que o problema pede pra a gente é o fator de forma entre a superfície interna e a abertura de cada uma!

Para facilitar vamos usar duas regrinhas! A primeira é a regra da soma:

F 1 - 2 + F 1 - 1 = 1

Mas se a superfície 1 , for a superfície aberta, então você concorda que não tem como ela incindir radiação sobre ela mesma? Então F 1 - 1 = 0 , logo:

F 1 - 2 = 1

A segunda é a regra da reciprocidade:

F 1 - 2 = A 2 A 1 F 2 - 1

Para a abertura:

1 = A 2 A 1 F 2 - 1

Isolando F 2 - 1 :

F 2 - 1 = A 1 A 2

Passo 2

Agora vamos aplicar isso nas formas que o enunciado da pra a gente!

  • Cone:

    • F 1 - 2 = 1

    E:

    F 2 - 1 = A 1 A 2

    A 1 é a área de uma circunferência:

    A 1 = π d 2 4

    A 2 é a área lateral de um cone, dada por:

    A 2 = π d 2 L 2 + d 2 2   1 2

    Substituindo:

    F 2 - 1 = π d 2 4 π d 2 L 2 + d 2 2   1 2 = d 2 L 2 + d 2 2   - 1 2

    E se a gente jogasse esse d pra dentro dos colchetes?!

    F 2 - 1 = 1 2 1 d 2 L 2 + d 2 2   - 1 2

    Ficamos com:

    F 2 - 1 = 1 2 L d 2 + 1 4   - 1 2

    Passo 3

  • Cilindro:

    • F 1 - 2 = 1

    F 2 - 1 = A 1 A 2

    A 1   é a área de uma circunferência:

    A 1 = π d 2 4

    A 2 é a área do interior do cilindro, dada pela soma das áreas da base e da lateral do cilindro:

    A 2 = π d 2 4 + π d L

    Então F 2 - 1 :

    F 2 - 1 = π d 2 4 π d 2 4 + π d L

    Isolando π d 2 4 :

    F 2 - 1 = π d 2 4 π d 2 4 1 + 4 L d

    Dando uma arrumadinha:

    F 2 - 1 = 1 + 4 L d - 1

    Passo 4

  • Esfera :

F 1 - 2 = 1

F 2 - 1 = A 1 A 2

A 1   é a área de uma circunferência:

A 1 = π d 2 4

A 2 é a área da esfera menos a área da abertura:

A 2 = π D 2 - π d 2 4

Substituindo:

F 2 - 1 = π d 2 4 π D 2 - π d 2 4

Isolando π d 2 4 :

F 2 - 1 = π d 2 4 π d 2 4 ( 4 D 2 d 2 - 1 )   = 1 ( 4 D 2 d 2 - 1 )

Dando uma arrumadinha:

F 2 - 1 = 4 D 2 d 2 - 1 - 1

Resposta

Os fatores de forma são:

Cone:

F 2 - 1 = 1 2 L d 2 + 1 4   - 1 2

Cilindro:

F 2 - 1 = 1 + 4 L d - 1

Esfera:

F 2 - 1 = 4 D 2 d 2 - 1 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A superfície de uma barreira de radiação voltada para uma parede negra quente, a 400 K, tem uma refletividade de 0,95. Fixada ao lado de trás da barreira há uma folha de material isolante com 25 mm de
O lado inferior de um disco com 400 mm de diâmetro é aquecido por um forno elétrico, enquanto o lado superior está exposto ao ar ambiente quiescente e a uma vizinhança, ambos a 300 K. O forno radiante
O tubo de chama de um sistema de aquecimento de água é constituído por um longo duto circular com diâmetro D = 0,07 m e temperatura Ts = 385 K, através do qual gases de combustão escoam a uma temperat
Um aquecedor radiante, que é usado em processos de tratamento de superfícies, é constituído por um longo elemento aquecedor com formato cilíndrico e diâmetro D1 = 0,005 m, com emissividade ε1 = 0,80.
Considere as condições do Problema 9.107. Levando em consideração a radiação, assim como a convecção através da cavidade preenchida com hélio, determine a taxa mássica de nitrogênio gasoso que é perdi