Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 122

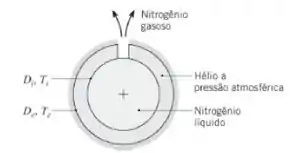
Considere as condições do Problema 9.107. Levando em consideração a radiação, assim como a convecção através da cavidade preenchida com hélio, determine a taxa mássica de nitrogênio gasoso que é perdida pelo sistema. As superfícies da cavidade são difusas e cinzas, com emissividades de εi = εe = 0,3. Se houver vácuo na cavidade, como as condições superficiais podem ser alteradas para reduzir ainda mais a evaporação? Justifique sua recomendação através de cálculos apropriados.

Passo 1

Animados para seguir que eu sei, não é?

Nós queremos achar aqui a taxa mássica de nitrogênio gasoso que é perdida pelo sistema, ok?

Bom, o sistema esta recebendo fluxo de calor radiante e convectivo que está sendo usado para evaporar o nitrogênio líquido:

q = q r a d + q c o n v = m ˙ h f g

Vamos abrir estas equações?

σ π D i 2 T e 4 - T i 4 1 ε i   + 1 - ε e ε e D i D e 2 + 4 π k e f f T i - T e 1 r i + 1 r e = m ˙ h f g

Vamos ver o que já temos?

D i = 1   m

D e = 1 , 1   m

ε i = ε e = 0,3

T i = 77   K

T e = 283   K

σ = 5,67 × 10 - 8 W m 2 K

Só precisamos achar o valor de k e f f !!

Sabendo que:

k e f f = 0,74 k   P r 0,861 + P r 1 4 R a s 1 4

Vamos lembrar também que:

R a s = g β T i - T e L s 3 v α

L s = 1 r i - 1 r e 4 3 2 1 3 r i - 7 5 + r e - 7 5 5 3

Para as propriedades do ar nós precisamos da temperatura média:

T m = T 1 + T 2 2 = 283 K + 77   K 2 = 1 8 0   K

Olhando na Tabela A – 4 para achar as propriedades do ar a uma temperatura a 180 K:

v = 51,3 × 10 - 6 m 2 s

α = 76,2 × 10 - 6 m 2 s

k = 0 , 107 W m K

β = 1 180 K

P r = 0 , 6 73

Substituindo:

L s = 1 0,5 - 1 0,55 4 3 2 1 3 0,5 - 7 5 + 0,55 - 7 5 5 3 = 0,0057

= 0,0016   m

R a s = 9,81 1 180 77 - 283 0,0057 3 76,2 × 10 - 6 51,3 × 10 - 6 = 529

k e f f = 0,74 0,107 0 , 6 73 0,861 + 0 , 673 1 4 52 9 1 4 = 0 , 30 9 W m K

Passo 2

Agora nós podemos achar o calor que é transferido para o nitrogênio:

q = 5,67 × 10 - 8 π 1 2 283 4 - 77 4 1 0,3   + 1 - 0,3 0,3 1 1,1 2 + 4 π 0,309 283 - 77 1 0,5 + 1 0,55

q = 4399   W + 216   W

q = 4 615   W

Agora sim !!

q = m ˙ h f g

Substituindo:

m ˙ = 4615   W 2 × 10 5 J k g = 0,023 k g s

Achamos assim nossa primeira resposta!!

Passo 3

Agora nós queremos saber se houver vácuo na cavidade, como as condições superficiais podem ser alteradas para reduzir ainda mais a evaporação?

Para isso nós podemos avaliar o fluxo radiante do passo 2, já que não há convecção, quando ε i = ε e varia de 0,1 até 0,9:

Então, quanto menor a emissividade menor a transferência de calor para o nitrogênio e, portanto, menor a perda de nitrogênio gasoso !!

E é isso aí galerinhaaa !!

Resposta

  1. m ˙ = 0,023 k g s
  2. M e n o r   a   e m i s s i v i d a d e ,   m e n o r   a   p e r d a   d e   n i t r o g ê n i o .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere discos negros, paralelos e coaxiais, separados por uma distância de 0,20m . O disco inferior, com diâmetro de 0 , 2 0m , é mantido a 500K , enquanto a vizinhança está a 3 1 0K .Qual será a t
Uma cavidade cilíndrica com diâmetro D e profundidade L é usinada em um bloco de metal, e as condições são tais que as suas superfícies da base e lateral são mantidas a T 1=95 0K e T 2 = 65 0K , respe
Considere as seguintes fendas, cada uma com largura W , que foram usinadas em um bloco de material sólido.(a) Para cada caso, obtenha uma expressão para o fator de forma da fenda com relação à vizinha
Oxigênio líquido é armazenado em um vaso esférico com parede delgada e 0 , 75m de diâmetro, que se encontra no interior de um segundo vaso esférico, também com parede delgada e com 1 , 1m de diâmetro.
Uma chapa de alumínio anodizado, com espessura de t = 5m m , é usada para descartar calor em um dispositivo de potência para uso no espaço. A borda da chapa é fixada à fonte quente e a chapa é mantida