Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 47
Um tubo circular, com diâmetro externo de 25 mm, é colocado em uma corrente de ar a 25 °C e 1 atm de pressão. O ar está em escoamento cruzado em relação ao tubo com uma velocidade de 15 m/s, enquanto a superfície externa do tubo é mantida a 100 °C. Qual é a força de arrasto exercida no tubo por unidade de comprimento? Qual é a taxa de transferência de calor saindo do tubo por unidade de comprimento?
Passo 1
Beleza! Vamos começar esse exercício calculando a temperatura de filme , dada pela média entre a temperatura do escoamento e a da superfície do tubo, então teremos:
Agora nós vamos recorrer à tabela A.4 do apêndice A para encontrar as propriedades do ar na temperatura de filme para utilizar posteriormente nos cálculos. Então, através da tabela A.4 conseguimos os seguintes dados:
Tá legal! Sabendo que a força de arrasto é dada pela equação:
No nosso caso a área de contato será a área lateral do cilindro, que é dada por:
Substituindo essa expressão na equação anterior, temos:
E, dividindo ambos os lados por L, obtemos a força de arrasto por unidade de comprimento no tubo, que será:
Passo 2
Agora nós vamos recorrer à Figura 7.9 apresentada nessa seção do livro, onde temos a relação entre o coeficiente de arrasto e o número de Reynolds do escoamento para diferentes geometrias:
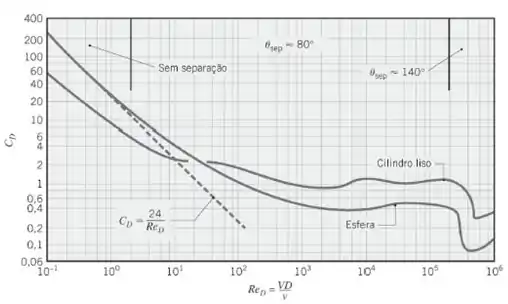
Então, para encontrar o coeficiente de arrasto, precisamos do número de Reynolds, que será:
Com esse número de Reynolds, e como temos um cilindro liso, com o auxílio da figura acima, teremos um coeficiente de arrasto igual a:
Então, substituindo os valores conhecidos na equação para a força de arrasto descrita no passo 1, teremos:
Passo 3
Agora, para avaliar a taxa de transferência de calor saindo do tubo por unidade de comprimento, precisamos calcular o número de Nusselt, depois encontrar o coeficiente convectivo, para só então calcular o calor trocado. Então, para calcular o Nusselt, nós iremos utilizar a relação de Hilpert, dada pela equação 7.52 a seguir:
Em que os coeficientes C e m são dados na tabela 7.2 a seguir:
Então, para o nosso número de Reynolds, teremos:
Substituindo esses valores na equação para Nusselt, temos:
Sabendo que o coeficiente convectivo se relaciona com Nusselt através da seguinte equação:
Podemos substituir os valores conhecidos e encontrar o valor do coeficiente convectivo, então teremos:
E, finalmente, a taxa de transferência de calor por convecção por comprimento do tubo será dada por: