Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 104

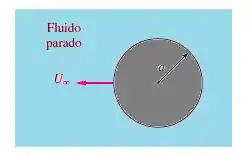
Considere um cilindro de raio a movendo-se à velocidade U ∞ através de um fluido parado, como na figura abaixo. Trace as linhas de corrente relativas ao cilindro, modificando a equação 8.37 para obter o escoamento relativo com K = 0 . Integre para encontrar a energia cinética relativa total e verifique a massa hidrodinâmica de um cilindro da equação 8.104.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)! Para esse problema 2D, a massa de forma diferencial pode ser escrita como sendo:

d m = ρ b r   d r d θ

Quando b é a espessura para dentro do papel.

Passo 2

Subtraindo da linha de corrente U, nós temos que:

V r ​ r e l = - U c o s θ a 2 r 2

V θ ​ r e l = - U s e n θ a 2 r 2

Passo 3

Ou seja, as velocidades “relativas” são de fato as velocidades induzidas. Agora, introduzimos um elemento de energia cinética dentro da equação 8.102 e integrar!!!

K E = ∫ 1 2 d m   V r e l 2 = ∫ 0 2 π ∫ a ∞ 1 2 ρ b r   d r   d θ U c o s θ a 2 r 2 2 + U   s e n θ a 2 r 2 2 = π 2 ρ U a 2 b

Por definição temos que m h i d r o = K E U 2 2 = π ρ a 2 b = massa desprendida do cilindro.

Resposta

m h i d r o = π ρ a 2 b  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.35 Exemplo 5.6 pelo campo de velocidade V → = r ω e ^ θ . Determine a função de corrente para este escoamento. Avalie a vazão em um volume por unidade de profundidade entre r 1 = 0,10m e r 2 = 0,12m
5.36 Em um escoamento unidimensional e paralelo na direção positiva de x , a velocidade varia lineramente de zero em y = 0 até 30m / s em y = 1,5m . Determine uma expressão para a função de corrente,
Mostre por expansão e separando os termos real e imaginário que f = z 6 (em que z é o número complexo z = x + i y ) conduz a um potencial de velocidade válido (a parte real de f ) e a uma função de co
Considere o escoamento em torno de um cilindro circular com velocidade de corrente livre da direita para a esquerda e um vórtice livre de sentido anti­horário. Mostre que a força de sustentação sobre
Um modelo grosseiro de um tornado é formado pela combinação de um sorvedouro, de intensidade q = 2800m 2 / s , e um vórtice livre, de intensidade K = 5600m 2 / s . Obtenha a função de corrente e o pot