Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 56

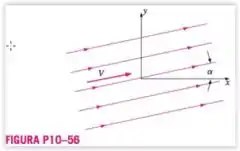
Considere uma corrente uniforme de intensidade V inclinada com um ângulo a (Figura P 10 - 56 ). Supondo escoamento irrotacional incompressível planar, determine a função potencial de velocidade e a função de corrente. Mostre todo o seu trabalho.

Passo 1

Oioi, xentê! Nessa questão vamos determinar a função potencial de velocidade e a função de corrente mas de uma forma diferente pois agora temos uma ilustração em que apresenta intensidade V inclinada com um ângulo a . Go!

Começamos buscando nossas componentes em coordenadas cartesianas:

u = ∂ ϕ ∂ x = ∂ ψ ∂ y = V cos ⁡ a

v = ∂ ϕ ∂ y = - ∂ ψ ∂ x = V sin ⁡ a

Em relação a x temos x = V cos ⁡ a , uma vez que o ângulo é próximo do cateto adjacente; e para y temos V sin ⁡ a , pois é próximo do cateto oposto.

Passo 2

Agora integramos o primeiro componente para isolar ϕ :

∂ ϕ = u   d x       ∴       ∫ 1 d ϕ = ∫ V cos ⁡ a     d x         ∴             ϕ = V x cos ⁡ a   + f ( y )

Assim, podemos diferenciar o resultado em relação a y , gerando a função:

∂ ϕ ∂ y = f ' y = v = V sin ⁡ a

Integramos:

f y = ∫ V sin ⁡ a d y

f y = V y sin ⁡ a + C

Unindo os componentes:

ϕ = V x cos ⁡ a + V y sin ⁡ a

Passo 3

Por fim, fazemos o mesmo para a função corrente, o primeiro componente para isolar ψ :

∂ ψ = u   d y       ∴       ∫ 1 d ψ = ∫ V cos ⁡ a     d y         ∴             ψ = V y cos ⁡ a   + g ( x )

Assim, podemos diferenciar o resultado em relação a y , gerando a função:

∂ ψ ∂ x = - g ' ( x ) = - v = - V sin ⁡ a

Integramos:

g x = - ∫ V sin ⁡ a d x

g x = - V x sin ⁡ a + C

Unindo os componentes:

  ψ = V y cos ⁡ a - V x sin ⁡ a

Prontinho!!

Resposta

ϕ = V x cos ⁡ a + V y sin ⁡ a

ψ = V y cos ⁡ a - V x sin ⁡ a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.49 Resolva o Problema 4.123 para msotrar que a velocidade radial na folga estreita é V r = Q / ( 2 π r h ) . Deduza uma expressão para a aceleração de uma partícula fluida na folga.
5.73 Um escoamento é representado pelo campo de velocidade V → = x 7 - 21 x 5 y 2 + 35 x 3 y 4 - 7 x y 6 i ^ + ( 7 x 7 y - 35 x 4 y 3 + 21 x 2 y 5 - y 7 ) j ^ . Determine se o campo é (a) um possível
5.69 Quais, se existir algum, dos seguintes campos de escoamento são irrotacionais?(a) u = 2 x 2 + y 2 - x 2 y ; v = x 3 + x y 2 - 2 y (b) u = 2 x y - x 2 + y ; v = 2 x y - y 2 + x 2 (c) u = x t + 2 y
5.76 Considere o campo de escoamento representado pela função de corrente ψ = 3 x 5 y - 10 x 3 y 3 + 3 x y 5 . Esse é um possível escoamento bidimensional incompressível? O escoamento é irrotacional?
5.59 Um perfil de velocidade aproximadamente linear foi usado no Problema 5.10 para modelar uma camada-limite laminar e incompressível sobre uma placa plana. Para este perfil, obtenha expressões para