Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 15

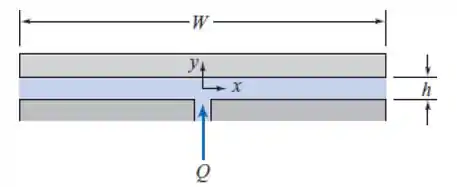
Um macaco hidráulico suporta uma carga de 50.000 N/m por pé de comprimento perpendicular ao diagrama. O mancal é alimentado com óleo SAE 10W – 30 a 35°C e 700 kPa através do rasgo central. Como o óleo é viscoso e a folga é estreira, o escoamento na folga pode ser considerado completamente desenvolvido. Calcule (a) a largura requerido para a plataforma do mancal, (b) o gradiente de pressão resultante, dp/dx, e (c) a altura h da folga, se Q = 1   m L / m i n / m .

Passo 1

Tá legal, podemos tratar esse exercício como sendo um escoamento laminar com gradiente de pressão entre placas estacionárias e paralelas, e dessa forma, utilizar a equação 8.6c vista nesse capítulo, então, temos:

Q l = a 3 Δ p 12 μ L

Isolando a altura a = h , temos:

Q l = h 3 Δ p 12 μ L → h = 12 Q μ L l Δ p 1 3

Tá legal, então, nesse caso, vamos assumir que temos escoamento laminar, e dessa forma, o gradiente de pressão será constante, de forma que a equação para a pressão é linear. Com isso, assumindo uma pressão de entrada p e e sabendo que temos descarga para a atmosfera, onde p s = p a t m podemos considerar p s = 0 e obter o valor da pressão em seu valor manométrico, dessa forma, a equação para o perfil de pressão pode ser escrita como:

p x = p e 1 - 2 x W

Note que para x = 0 temos p = p e e para x = W / 2 (ponto de descarga), temos p = 0 .

Passo 2

Com a expressão para a pressão em função de x , podemos encontrar a força exercida no pistão integrando essa expressão na distância, então, temos:

F = ∫ p d x = ∫ - W 2 W 2 p e 1 - 2 x W d x

Agora, integrando essa expressão, temos:

F = p e x - x 2 W - W 2 W 2

Substituindo os limites de integração, temos:

F = p e W 2 - 1 W W 2 2 - - W 2 - 1 W - W 2 2

F = p e W 2 - W 4 - - W 2 - W 4 → F = p e W 4 + 3 W 4 → F = p e W

Então, isolando a distância W dessa equação e substituindo os valores conhecidos, temos:

W = F p e = 50000 700.10 3 → W = 0,071   m

Passo 3

Dessa forma, o gradiente de pressão será:

d p d x = - Δ p W 2

Substituindo os valores conhecidos, temos:

d p d x = - 700.10 3 0,071 2 → d p d x = - 19718,3   k P a / m

Passo 4

Então, agora, retornando à equação do passo 1 para a altura h temos:

h = 12 Q μ L l Δ p 1 3

Consultando o valor de μ na tabela do apêndice A do livro, chegamos em:

μ = 0,07   N . s / m 2

Então, substituindo todos os valores conhecidos na equação para h , temos:

h = 12 1.10 - 6 0,07 0,071 2 700.10 3 1 3 → h = 3,49.10 - 5   m

Resposta

W = 0,071   m

d p d x = - 19718,3   k P a / m

h = 3,49.10 - 5   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o sistema série-paralelo da figura a seguir, todos os tubos são de ferro fundido asfaltado de 8 cm de diâmetro. Se a queda total de pressão p 1 - p 2 = 750k P a , determine a vazão resultante Q e
Modifique o problema P6.113 da seguinte maneira: Considere a bomba ligada e deixando 45 kW para a vazão no tubo 2. O fluido é gasolina a 20°C. Determine (a) a vazão em cada tubo e (b) a queda de press
O sistema de tubos de aço galvanizado em paralelo da figura abaixo fornece água a 20°C com uma vazão total de 0, 036 m³/s. Se a bomba está totalmente aberta, mas desligada, com um coeficiente de perda
Na figura abaixa, encontram-se 38 m de tubo de 50 mm, 23 m de tubo de 150 mm e 46 m de tubo de 75 mm, todos de ferro fundido. Há também três cotovelos de 90° e uma válvula globo aberta, todos flangead
O sistema de três reservatórios da figura abaixo fornece água a 20°C. Os dados do sistema são: D 1 = 200m mD 2 = 150m m D 3 = 225m m L 1 = 549m mL 2 = 366m mL 3 = 488m m Todos os tubos são de aço galv