Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 179

Um disco de massa m é restringido horizontalmente, mas está livre para movimentar na vertical. Um jato de água atinge o disco por baixo. O jato sai do bocal com velocidade inicial V 0 . Obtenha uma equação diferencial para a altura variável do disco, h t , acima do plano de saída do jato, se o disco for largado na horizontal de uma altura, H . (Você não poderá resolver essa equação, pois ela é altamente não linear!) Considere que, quando o disco atinge o equilíbrio, a sua altura acima do plano de saída do bocal é h 0 .

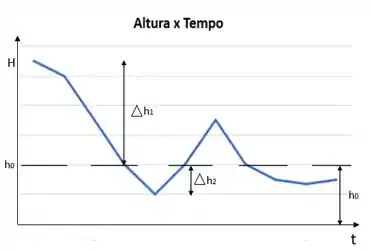
  1. Esboce um gráfico de h ( t ) para o disco liberado em t = 0 partindo de H > h 0 ;
  2. Explique por que a curva h ( t ) tem o aspecto encontrado.

Passo 1

Equações:

  1. Bernoulli:

    2. p 0 p g + V 0 2 2 g + z 0 = p 1 p g + V 1 2 2 g + z 1

  2. Momento do Momento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante ( V = V 1 - U ) ;
  4. Escoamento uniforme.
  5. Força de resistência desprezível;
  6. p 0 = p 1 = p a t m ;
  7. z 0 = 0 .

Passo 2

Pelas considerações feitas no Passo 1, temos:

- m g - a r y m = v 1 [ - ρ V 1 - U A 1 ] + v 2 [ ρ V 2 - U A 2 ]

Sendo:

v 1 = V 1 - U ;

v 2 = 0 ;

a r y = d 2 h d t 2 ;

U = d h d t .

Temos:

- m g - d 2 h d t 2 m = - ρ V 1 - d h d t 2 A 1

Da equação de Bernoulli, temos:

V 0 2 2 g = V 1 2 2 g + z 1

Com z 1 = h , temos:

V 1 = V 0 2 - 2 g h

Pela continuidade:

V 0 A 0 = V 1 A 1 → A 1 = A 0 V 0 V 1  

Substituindo na equação principal:

- m g - d 2 h d t 2 m = - ρ V 0 2 - 2 g h - d h d t 2 A 0 V 0 V 0 2 - 2 g h

Rearranjando:

d 2 h d t 2 = ρ V 0 2 - 2 g h - d h d t 2 A 0 m   V 0 V 0 2 - 2 g h - g

Passo 3

Na altura de equilíbrio, h = h 0 , d h d t = 0 e d 2 h d t 2 = 0 , assim:

ρ V 0 2 - 2 g h 0   A 0 V 0 - m g = 0

V 0 2 - 2 g h 0 = m g ρ A 0 V 0 2

Isolando h 0 :

h 0 = V 0 2 2 g - 1 2 g m g ρ A 0 V 0 2

h 0 = 1 2 g V 0 2 - m g ρ A 0 V 0 2

Passo 4

Fazendo H > h 0 e d h d t = 0 .

Como as equações para d 2 h d t 2 são não lineares, ocorrerão oscilações.

O comportamento gráfico esperado é esboçado abaixo:

Resposta

h 0 = 1 2 g V 0 2 - m g ρ A 0 V 0 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.105 Um fluido com massa específica ρ = 750k g / m 3 escoa ao longo de uma placa plana de largura 1 m. A velocidade da corrente livre, não perturbada, é U 0 = 10m / s . Em L = 1m a jusante da borda d
4.104 Considere o escoamento incompressível de um fluido em uma camada-limite como descrito no Exemplo 4.2. Mostre que a força de arrasto devido ao atrito do fluido sobre a superfície é dada por F f =
4.108 Os gases saindo do bocal de propulsão de um foguete são modelados como se escoassem radialmente para fora a apartir de um ponto a montante da garganta do bocal. Considere que a velocidade do esc
4.103 Ar entra em um duto, de diâmetro D = 25,0m m , por uma entrada bem arredondada com velocidade uniforme, U 1 = 0,870m / s . Em uma seção a jusante, onde L = 2,25m , o perfil de velocidade interma
4.107 Uma placa divisora de jato, de borda viva, inserida parcialmente em uma corrente plana de água, produz o padrão de escoamento mostrado. Analise a situação de modo a avaliar θ como uma função de