Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 125
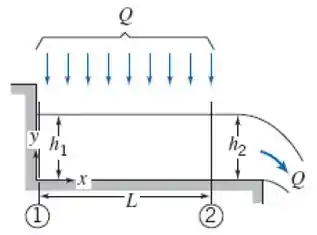
Um líquido cai verticalmente dentro de um canal retangular aberto, curto e horizontal, de largura . A vazão volumétrica total, , é uniformemente distribuída sobre a área . Despreze efeitos viscosos. Obtenha uma expressão para em termos de e . Sugestão: Escolha um volume de controle com fronteira externa localizada em . Esboce o perfil da superfície, . Sugestão: Use um volume de controle diferencial de largura .
Passo 1
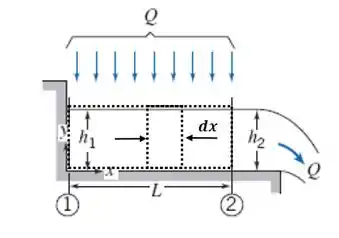
Tá legal! Vamos começar esse exercício ilustrando o problema e desenhando os dois volumes de controle sugeridos no enunciado:
Vamos começar esse exercício aplicando o princípio da continuidade para o sistema, nesse caso, teremos:
Então, nesse caso, teremos regime permanente, então a derivada no tempo será zero. Aplicando para o volume de controle com fronteira externa localizada em , temos:
Passo 2
Agora vamos aplicar a equação para o equilíbrio de momento para esse mesmo volume de controle, então aplicando a equação na direção , temos:
Nesse caso, temos regime permanente, então o termo com a derivada no tempo será zero. Como não temos forças gravitacionais agindo na direção , então . Dessa forma a equação se torna:
Só que, nesse caso, sabemos que , então a equação acima se torna:
No entanto, conforme vimos no passo 1, a velocidade será:
Então, substituindo essa expressão na equação anterior, temos:
E, isolando dessa equação, temos:
Passo 3
Agora, para esboçar o perfil da superfície , vamos analisar o volume de controle diferencial de largura ilustrado no esquema do passo 1. Aplicando a conservação de massa, temos:
Então, nesse caso, teremos regime permanente, então a derivada no tempo será zero. Aplicando para o volume de controle diferencial, temos:
Então, como sabemos que a multiplicação de dois infinitesimais dá um número bem pequeno, então, podemos ignorar esse termo, e a equação se torna:
Agora, vamos utilizar a propriedade do produto da derivada, só que para voltar ao estado original, então, temos:
Passo 4
Agora vamos aplicar a equação para o equilíbrio de momento para esse mesmo volume de controle, então aplicando a equação na direção , temos:
Nesse caso, temos regime permanente, então o termo com a derivada no tempo será zero. Como não temos forças gravitacionais agindo na direção , então . Dessa forma a equação se torna:
E, nesse caso, sabemos que , e , então a equação acima se torna:
Da continuidade, temos que , então, simplificando os termos e substituindo essa relação, temos:
Então, como sabemos que a multiplicação de dois infinitesimais dá um número bem pequeno, então, podemos ignorar esses termos, e a equação se torna:
No desenvolvimento da equação da continuidade, temos que:
Então, substituindo essa expressão na equação anterior:
Colocando o termo em evidência no denominador para podermos interpretar a equação, temos:
Então, pelo desenho, podemos ver que e a altura vai diminuindo com o comprimento , dessa forma a derivada deve ser menor que zero, para isso, devemos ter:
Já que os outros termos da equação são todos positivos.