Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 5

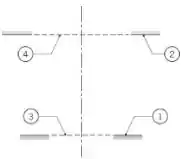
Considere os dois discos em forma de anel, coaxiais e paralelos, mostrados na figura.

Mostrar que F 12 pode ser representado por,

F 1 2 = 1 A 1 { A 1,3 F 1,3 2,4 - A 3 F 3 2,4 - A 4 F 4 1,3 - F 41 }

Com todos os fatores de forma no lado direito da equação podendo ser determinados na Figura 13.5 ou na Tabela 13.2 para discos coaxiais paralelos.

Passo 1

Oieeee, vamos ver o que temos nessa questãozitcha?! Aqui temos dois discos paralelos, coaxiais e em forma de anel. E com eles, queremos mostrar que o fator de exibição F 12 pode ser expresso como:

F 12 = 1 A 1 { A 1,3 F 1,3 2,4 - A 3 F 3 2,4 - A 4 F 4 1,3 - F 41 }

Com todos os fatores de forma no lado direito da equação podendo ser determinados na Figura 13.5 ou na Tabela 13.2 para discos coaxiais paralelos.

Passo 2

Para resolver essa questão vamos assumir superfícies difusas com radiosidades uniformes. Usando a regra aditiva, onde o parêntese denota uma superfície composta, temos:

F 1 ( 2,4 ) = F 12 + F 14

F 1 2 = F 1 ( 2,4 ) + F 14

Relação para F 1 ( 2,4 ) :   Usando a regra aditiva

A 1,3 F 1,3 2,4 = A 1 F 1 2,4 - A 3 F 3 2,4

Onde a marca de seleção denota um F i j que pode ser avaliado usando a Fig. 13.5 para discos paralelos coaxiais.

Relação para F 14 : Aplicar reciprocidade,

A 1 F 14 = A 4 [ F 4 1 , 3 - F 43 ]

Relação para F12: Substituindo as equações,

F 12 = 1 A 1 { A 1,3 F 1,3 2,4 - A 3 F 3 2,4 - A 4 F 4 1,3 - F 41 }

Por fim, conseguimos chegar onde a questão nos pediu! 😊

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Revestimentos aplicados a longas tiras metálicas são curados pela instalação das tiras ao longo das paredes de um longo forno com seção transversal quadrada.As condições térmicas no interior do forno
Uma chapa de alumínio anodizado, com espessura de t = 5m m , é usada para descartar calor em um dispositivo de potência para uso no espaço. A borda da chapa é fixada à fonte quente e a chapa é mantida
Um fluido criogênico escoa por um tubo com 20m m de diâmetro, cuja superfície externa é difusa e cinza, com uma emissividade de 0,05 e uma temperatura de 77K . Esse tubo é concêntrico a um tubo maior,
Considere o sistema de descarte de calor em espaçonaves do Problema 13.20, mas sob condições nas quais as superfícies 1 e 2 não podem ser aproximadas por corpos negros.Para superfícies isotérmicas com
Um fluido criogênico escoa por um tubo com 20m m de diâmetro, cuja superfície externa é difusa e cinza, com uma emissividade de 0,0 5 e uma temperatura de 77K . Esse tubo é concêntrico a um tubo maior