Um cone circular e um cilindro circular com o mesmo diâmetro e comprimento estão posicionados coaxialmente, a uma distância , de um disco circular como mostrado no esquema. As superfícies da base e da lateral internas do cilindro podem ser tratadas como uma superfície única, . A área hipotética correspondente à abertura do cone e do cilindro é identificada por .

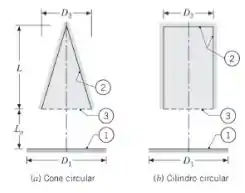
(a) Mostre que, para os dois arranjos, e sendo o fator de forma entre dois discos paralelos coaxiais (Tabela 13.2).

(b) Para e , calcule e para as configurações cônica e cilíndrica e compare seus valores relativos. Explique quaisquer similaridades e diferenças.

(c) Os valores relativos de e variam nas configurações cônica e cilíndrica quando aumenta e todos os outros parâmetros permanecem fixos? No limite de muito grande, o que você espera que aconteça? Esboce as variações de e com e explique as características marcantes.

Para resolver essa questão vamos assumir superfícies difusas com radiosidades uniformes e superfícies internas da base e laterais do cilindro tratadas como uma superfície única, . Para ambas as configurações,

Uma vez que a potência radiante que sai de que é interceptada por também é interceptada por . Aplicando reciprocidade entre e ,

Resolvendo para , encontramos:

Ao tratar o cone e o cilindro como gabinetes de duas superfícies, a regra de soma para é,

Aplicando a reciprocidade entre e , encontramos:

E desde , encontramos:

Para os valores especificados de e , os fatores de visualização são calculados e tabulados abaixo. As relações para as áreas são:

Cone do disco:

Cilindro de disco:

O fator de visualização é avaliado na Tabela 13.2, discos paralelos coaxiais (Fig. 13.5) e encontramos .

Cone do disco:

Cilindro de disco:

Daqui temos que é maior para o cone do disco do que para o cone do cilindro. Ou seja, para (a), a superfície vê mais de e menos de si mesma do que para (b). Observe que é maior para (b) que (a), isso é uma conseqüência de .