Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 62

Um forno está localizado próximo a um denso conjunto de tubos de transporte de um fluido criogênico. O conjunto de tubos cobertos por gelo formam aproximadamente uma superfície plana com uma temperatura média de Tt = 0°C e uma emissividade de εt = 0,6. A parede do forno tem uma temperatura de Tf = 200°C e uma emissividade de εf = 0,9. Para proteger o equipamento de refrigeração e a tubulação de uma carga térmica em excesso, barreiras de radiação de alumínio refletivas com uma emissividade de εb = 0,1 são colocadas entre os tubos e a parede do forno, como mostrado na figura. Considere todas as superfícies difusas e cinzas.

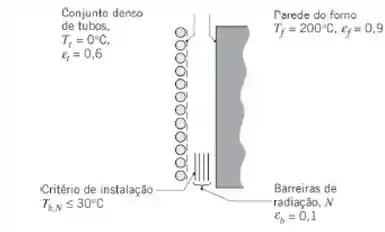
Se a temperatura da barreira mais próxima dos tubos Tb,N tem que ser inferior a 30°C, quantas barreiras de radiação, N, devem ser instaladas entre os tubos e a parede do forno?

Passo 1

Vamos lá!! Temos um forno e um conjunto denso de tubos posicionados paralelamente entre si, como se fossem duas placas paralelas! Entre eles tem N barreiras e a gente quer justamente saber qual é a quantidade de barreiras existentes!

Mas com uma condição, a última barreira deve ter temperatura menor ou igual a 30 ℃ !

Vamos escrever q f t tendo em mente que elas se comportam como duas placas paralelas:

q f t = σ T f 4 - T t 4 1 A f ε f + 1 A t ε t - 1 + f ( ε b )

Aqui f ( ε b ) representa a resistência dessas N placas, que também estão dispostas paralelamente, podemos dizer que a resistência de cada placa é:

R b = 2 × 1 A b ε 2 - 1

Considerando os dois lados da placa com emissividade iguais! A resistência de N placas é:

R b N = N 2 A b ε 2 - 1

Substituindo em q f t :

q f t = σ T f 4 - T t 4 A f 1 ε f + 1 ε t - 1 + N 2 ε b - 1

O problema é que não conhecemos nem q f t nem N , então precisamos de outra equação!!

Conhecemos a temperatura máxima da última placa, T b n = 30 ℃ , então podemos calcular a transferência de calor entre a última placa e os tubos nessa temperatura!

q b n   t = σ T b , n 4 - T t 4 A f 1 ε b + 1 ε t - 1

Passo 2

Considerando um sistema permanente, temos:

q f t = q b n t

Maaas, a gente tem como calcular q b n t a gente pode calcular q b n t m á x

q f t ≤ q b n t m á x  

Substituindo:

σ T f 4 - T t 4 A f 1 ε f + 1 ε t - 1 + N 2 ε b - 1 ≤ σ T b , n 4 - T t 4 A f 1 ε b + 1 ε t - 1

Podemos cortar os termos repetidos:

T f 4 - T t 4 1 ε f + 1 ε t - 1 + N 2 ε b - 1 ≤ T b , n 4 - T t 4 1 ε b + 1 ε t - 1

E isolar N :

N ≥ 1 ε b + 1 ε t - 1 T b , n 4 - T t 4 T f 4 - T t 4 - 1 ε f + 1 ε t - 1 1 2 ε b - 1

Passo 3

Vamos relebrar os dados do enunciado, e converter eles pro S I se necessário:

ε b = 0,1

ε t = 0,6

ε f = 0,9

T b , n = 30 ℃ + 273 = 303   K

T t = 0 + 273 = 273   K

T f = 200 ℃ + 273 = 473   K

Substituindo:

N ≥ 1 0,1 + 1 0,6 - 1 303 4 - 274 4 473 4 - 273 4 - 1 0,9 + 1 0,6 - 1 1 2 0,1 - 1

Calculando:

N ≥ 8,6

Como o número de barreiras precisa ser inteiro:

N = 9

Uhuuuul!!

Resposta

N = 9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois projetos de forno, como ilustrados e dimensionados no Problema 13.4, são usados para aquecer um corpo de prova em forma de disco ( A 1 ) . A potência fornecida aos fornos cônico e cilíndrico ( A
Um aquecedor tubular com a superfície interna negra de temperatura uniforme T s =1000K irradia um disco que se encontra em posição coaxial ao tubo.(a) Determine a potência radiante oriunda do aquecedo
Uma peça longa em forma de V é tratada termicamente pela sua suspensão no interior de um forno tubular com um diâmetro de 2m e uma temperatura de parede de 1000K . O V tem os lados com 1m de comprimen
Uma placa circular com 500m m de diâmetro é mantida a T 1=600K e está posicionada coaxialmente a uma peça com formato cônico. O lado superior do cone é isolado termicamente. A placa e o cone, cujas su
Um sensor de fluxo térmico com 4m m de diâmetro está posicionado normal e a 1m de distância da abertura, com 5m m de diâmetro, de um forno a 1000K que se comporta como um corpo negro. A cobertura que