Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 110
O isolamento térmico composto mostrado na figura, que foi descrito no Capítulo 1 (Problema 1.86e), está sendo cogitado como material para um teto.
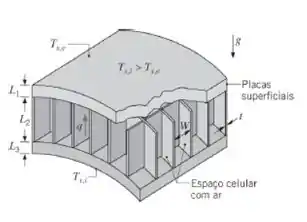
Foi proposto que as placas externa e interna sejam feitas com material aglomerado de baixa densidade, com espessuras L1 = L3 = 12,5 mm, e que o núcleo com estrutura de colmeia seja construído com placas aglomeradas de alta densidade. As células quadradas do núcleo devem ter um comprimento L2 = 50 mm, largura W = 10 mm e espessura de parede t = 2 mm. A emissividade das duas placas aglomeradas é aproximadamente 0,85 e as células da colmeia são preenchidas com ar a uma pressão de 1 atm. Para avaliar a efetividade do isolante, sua resistência térmica total deve ser determinada sob condições operacionais representativas, nas quais a temperatura da superfície inferior (interna) é Ts,i = 25°C e a temperatura da superfície superior (externa) é Ts,e = –10°C. Para avaliar o efeito da convecção natural no espaço contendo ar, considere uma diferença de temperatura na célula de 20°C e avalie as propriedades do ar a 7,5°C. Para avaliar o efeito da radiação através do espaço contendo ar,
admita temperaturas nas superfícies internas das chapas externa e interna de –5 e de 15°C, respectivamente.
Passo 1
Vamos que vamos galerinha !!
Bom, nós temos que achar resistência térmica total, certo?
Para isso vamos ver as resistências atuando aqui, com condução ocorrendo nas placas e condução, convecção e fluxo radiante entre elas!!
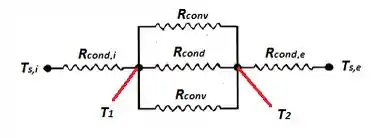
Para a resistência total:
Para as resistências em paralelo:
Vamos começar olhando cada uma delas:
Para a condução que ocorre nas placas aglomeradas:
As outras nós vamos deixar para depois de propósitoo !!
Vamos ver nossos dados?
Para a temperatura de 7,5°C, ou seja, 280,5 K, olhamos na Tabela A – 3 para as placas:
E para o ar, a Tabela A – 4:
Substituindo:
Passo 2
A próxima resistência é a convecção que ocorre no espaço entre as placas:
Para achar o coeficiente convectivo vamos usar a fórmula:
Vamos lembrar também que:
Então:
Substituindo:
Agora ficou fácil, basta substituirmos:
Passo 3
Para achar a resistência ao fluxo radiante deverá ser calculada usando o calor:
Lembrando que:
É importante nós observarmos aqui que, para o fator de forma, usando o somatório:
Substituindo:
Mexendo um pouco na temperatura:
E agora vamos colocar na resistência:
O que nos falta é o fator forma aqui !!
Olhando a figura:
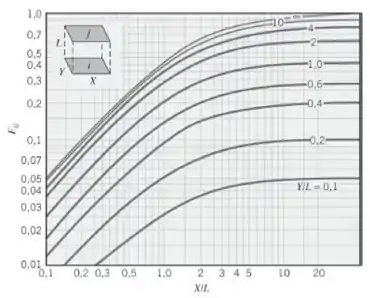
E fazendo a razão:
Olhando no gráfico:
E agora, substituindo:
Passo 4
Agora é só achar o total:
E no total:
E fechamos mais uma galerinha !!