Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 109

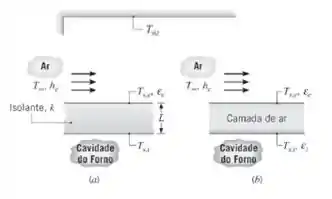
Opções para proteger termicamente o teto superior de um grande forno incluem o uso de um material isolante com espessura L e condutividade térmica k, caso (a), ou uma camada de ar com espessura equivalente formada pela instalação de uma folha metálica acima do teto, caso (b).

  1. Desenvolva modelos matemáticos que possam ser usados para avaliar qual das duas opções é a melhor. Em ambos os casos, a superfície interna é mantida na mesma temperatura T s , i , e o ar ambiente e a vizinhança estão a temperaturas equivalentes ( T ∞   =   T v i z ).
  2. Se k   =   0,090 W m K ,   L   =   25   m m ,   h e   =   25 W m 2 K , as superfícies são difusas e cinzas, com εi = εe = 0,50; T s , i =   900   K e T ∞   =   T v i z 300   K , quais são a temperatura da superfície externa T s , e e a perda de calor, por unidade de área superficial, associada a cada opção?
  3. Para cada caso, avalie os efeitos das propriedades radiantes da superfície sobre a temperatura da superfície externa e sobre a perda de calor por unidade de área, para εi = εe variando entre 0,1 e 0,9. Represente graficamente os seus resultados.

Passo 1

Animados para seguir que eu sei, não é?

Na letra (a) nós queremos achar os modelos matemáticos, ok?

No caso (a) a condução dentro do isolante está sendo transmitida pelo exterior na forma de convecção e fluxo radiante:

q " c o n d = q " c o n v + q " r a d

Substituindo:

k L T s , i - T s , e = h e T s , e - T v i z + ε e σ T s , e 4 - T v i z 4

Agora, no caso (b) nós teremos convecção e fluxo radiante na parte interna e externa :

h i T s , i - T s , e + σ T s , i 4 - T s , e 4 1 ε i   + 1 ε e - 1 = h e T s , e - T v i z + ε e σ T s , e 4 - T v i z 4

Mas ainda temos que achar h i ! Para isso basta nós usarmos a fórmula:

h i = k L 0,069 R a L 1 3 P r 1 3

Lembrando que:

R a L = g β T s , i - T s , e L 3 v a

Então o modela será:

k L 0,069 g β T s , i - T s , e L 3 v a 1 3 P r 1 3 T s , i - T s , e + σ T s , i 4 - T s , e 4 1 ε i   + 1 ε e - 1 = h e T s , e - T v i z + ε e σ T s , e 4 - T v i z 4

Finalizamos a letra (a) !!

Passo 2

Beleza, a letra (b) nos pede a temperatura da superfície externa T s , e e a perda de calor, por unidade de área superficial, associada a cada opção, ok?

Sabendo que:

k   =   0,090 W m K

L   =   25   m m

h e   =   25 W m 2 K

T s , i =   900   K

T ∞   =   T v i z 300   K

No caso (a) tá fácil:

0,055 0,025 900 - T s , e = 25 T s , e - 300 + 0,5 5,67 × 10 - 8 T s , e 4 - 300 4

T s , e = 366   K

E o fluxo de calor:

q " = 0,055 0,025 900 - 366 = 1920   W m 2

Bom, para o caso (b) vamos precisar das propriedades do ar, e para isso vamos ver a temperatura média:

T m = T s , i - T v i z 2 = 900   K - 300   K 2 = 730   K

Olhando a Tabela A – 4 e interpolando:

v = 7,62 × 10 - 6 m 2 s

k = 0,055 W m K

a = 1,09 × 10 - 4 m 2 s

P r = 0,702

β = 1 730 K

Substituindo:

0,055 0,025 0,069 9,81 1 730 300 - T s , e 0,025 3 7,62 × 10 - 6 1,09 × 10 - 4 1 3 0,702 1 3 900 - T s , e + 5,67 × 10 - 8 900 4 - T s , e 4 1 0,5   + 1 0,5 - 1 = 25 T s , e - 300 + 0,5 5,67 × 10 - 8 T s , e 4 - 300 4

T s , e = 598   K

E o fluxo de calor:

q " = 25 598 - 300 + 0,5 5,67 × 10 - 8 598 4 - 300 4

q " = 10849 W m 2

Passo 3

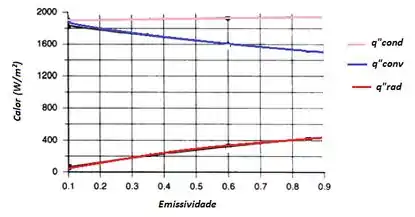
Para finalizar, a letra (d) nos pede para representar graficamente a variação das propriedades radiantes da superfície sobre a temperatura da superfície externa e sobre a perda de calor por unidade de área, para εi = εe variando entre 0,1 e 0,9!!

Repetindo o passo 2:

E é isso aí galerinhaaa !!

Resposta

  1. Caso (a): k L T s , i - T s , e = h e T s , e - T v i z + ε e σ T s , e 4 - T v i z 4

    2. Caso (b): k L 0,069 g β T s , i - T s , e L 3 v a 1 3 P r 1 3 T s , i - T s , e + σ T s , i 4 - T s , e 4 1 ε i   + 1 ε e - 1 = h e T s , e - T v i z + ε e σ T s , e 4 - T v i z 4

  2. Caso (a): T s , e = 366   K     |     q " = 1920 W m 2

    3. Caso (b): T s , e = 598   K     |     q " = 10849 W m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere as superfícies negras inclinadas ( A 1 e A 2 ), muito longas,mantidas nas temperaturas uniformes de T 1=1000K e T 2=800K . Determine a troca de radiação líquida entre as superfícies por unid
Água escoando através de um grande número de longos tubos circulares com paredes delgadas é aquecida por placas paralelas quentes, localizadas acima e abaixo da linha de tubos. Há vácuo no espaço entr
Um processo de fabricação exige o aquecimento de longos bastões de cobre, que são revestidos por uma fina película com ε = 1, colocando-os no interior de um grande forno, cuja superfície é mantida a 1
Muitos produtos são processados de uma maneira que requer uma temperatura do produto especificada como uma função do tempo. Considere um produto com a forma de um longo cilindro, com 10 mm de diâmetro
Um longo elemento aquecedor cilíndrico com 20 mm de diâmetro, operando a 700 K em meio ao vácuo, está posicionado a 40 mm de uma parede isolada de baixa condutividade térmica.Admitindo que o elemento