Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 107
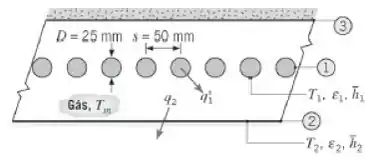
Uma linha de elementos aquecedores cilíndricos (1), regularmente espaçados, é usada para curar um revestimento superficial que está aplicado sobre um grande painel (2), posicionado abaixo dos elementos. Um segundo grande painel (3), cuja superfície superior é termicamente
isolada, encontra-se posicionado acima dos elementos. Os elementos são negros e mantidos a T1 = 600 K, enquanto o painel tem uma emissividade de ε2 = 0,5 e é mantido a T2 = 400 K. A cavidade é preenchida com um gás não participante e nas superfícies 1 e 2 ocorre transferência de calor por convecção, com e . (A convecção no painel com isolamento térmico pode ser desprezada).
- Determine a temperatura média do gás, Tm.
- Qual é a taxa, por unidade de comprimento axial, na qual a energia elétrica deve ser suprida a cada um dos elementos para mantê-los na temperatura especificada?
- Qual é a taxa de transferência de calor para uma fração do painel revestido que tem dimensões de 1 m de largura por 1 m de comprimento?
Passo 1
Shoow galerinhaa !! Vamos que vamos !!
A letra (a) nos pede para determinar a temperatura média do gás, .
Para isso nós precisamos do balanço de energia, ok? Nós temos transferência de convecção entre a superfície (1) e o gás e em seguida do gás para a superfície (2):
Nós sabemos que:
Shoow !! Se temos tudo só temos substituir:
Resolvendo:
Chegamos ao fim da letra (a), agora bora seguir !!
Passo 2
Bom, na letra (b) queremos saber a taxa, por unidade de comprimento axial, na qual a energia elétrica deve ser suprida a cada um dos elementos para mantê-los na temperatura especificada, ou seja, queremos !!
Vamos dar uma olhada no que está acontecendo:
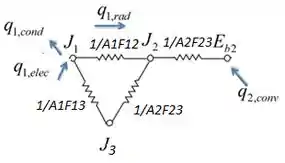
Como nós temos calor sendo transferido por convecção e como fluxo radiante:
O valor convectivo já até vimos:
Substituindo:
E o fluxo radiante:
Nós sabemos que:
A área também está fácil, nós já vimos no Passo 1 que:
Só precisamos da resistência equivalente, certo?
Vamos relembrar:
Se temos a área só precisamos achar os fatores deforma !!
Passo 3
Os fatores de forma são tabelados, não é? E neste caso podemos calcular e usando a fórmula:
Substituindo:
Fazendo o somatório para a superfície 2:
Por reciprocidade:
E ainda:
Agora podemos achar a resistência:
E agora o fluxo radiante:
Achando o fluxo elétrico:
Passo 4
Terminamos a (b) e já chegamos na letra (c) !!
Ela nos pediu para achar a taxa de transferência de calor para uma fração do painel revestido que tem dimensões de 1 m de largura por 1 m de comprimento!!
Como todo o calor adicionado pelos elementos aquecidos para a superfície (2):
Como nós temos 20 elementos:
E é isso aí galerinhaaa !!