Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 20
Um dreno pluvial circular de metal corrugado opera a meia seção com uma declividade de 0,76 m/km. Estime a descarga normal se o diâmetro do dreno for de 2,44 m.
Passo 1
Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Vamos desenhar nesse paranauê aí pra entender o que está sendo pedido, beleza?
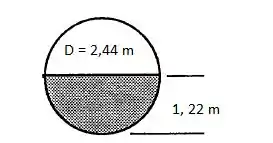
Novamente, o enunciado está pedindo pra gente estimar a descarga, ou seja, a vazão, então vamos usar a equação de Chézy:
Vamos já passar essa nossa declividade aí pra SI, ou seja, deixar isso m/m
Passo 2
Bora que bora, quem é a área desse treco aí?
Se a gente estivesse com todo o dreno cheio, seria toda a área, mas como temos metade, a área também deve ser reduzida em metade:
Passo 3
O perímetro também é moleza de calcular, certo? Porque qual é o comprimento de uma circunferência? ! Mas como temos METADE temos então que o comprimento, ou seja, perímetro é
Portanto, nosso raio hidráulico é:
Para um metal corrugado, o valor do coeficiente de rugosidade “n” é de 0,022
Passo 4
Substituindo na equação de Chézy, temos: