Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 2

Considere o escoamento estacionário da água através do bocal de uma mangueira de jardim assimétrico . Ao longo do eixo central do bocal, a velocidade da água aumenta de u e n t r a d a para u s a í d a conforme a ilustração. As medições revelam que a velocidade da água no eixo central aumenta parabolicamente através do bocal. Escreva uma equação para a velocidade no eixo central, u(x), com base nos parâmetros dados aqui, de X = 0 até X = L.

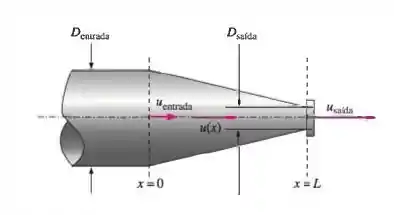
Passo 1

Bora lá! Vamos analisar a questão!

Toda massa que passa pelo ponto x = 0 (vamos chamar de ponto 1 pra simplificar) necessáriamente tem que passar pelo ponto x = L (esse a gente vai chamar de ponto 2). Certo?

O enunciado também diz que o sistema é estacionário, não tem acúmulo, logo:

m 1 ˙ = m 2 ˙

A vazão mássica no ponto 1 ( m ˙ 1 ) é igual a do ponto 2. A vazão mássica por sua vez é dada por:

m ˙ = ρ v A

Onde ρ é a densidade do fluido, v é a velocidade e A é a área da secção trasversal por onde o fluido passa. A área para dessa secção para a mangueira vai ser:

A = π R 2

Substituindo a expressão da área na vazão mássica e depois na igualdade entre as vazões mássicas, temos:

ρ u e n t r a d a π R 1 2 = ρ u s a i d a π R 2 2

Arrumando:

u s a i d a = u e n t r a d a R 1 2 R 2 2

Passo 2

Aqui a gente viu que a velocidade vai variar com o quadrado do raio! Mas essa expressão não da pra a gente o valor de uma velocidade em um ponto qualquer, ela apenas relaciona as duas velocidade em pontos conhecidos.

O enunciado disse para a gente que a velocidade varia de uma forma parabólica, então vamos dar uma olhada na expressão geral de uma parábola:

v = a x 2 + b x + c

Aqui, a e b são paramêtros com o qual a velocidade vai variar em relação a posição x e c é uma constante que independe da posição.

Maaas, como vimos no Passo 1 a velocidade varia apenas com um parâmetro, que é o raio da secção e na forma geral da parábola a velocidade varia com dois parâmetros ( a   e   b ) então um desses dois tem que ser igual a zero, certo?

Se a = 0 a gente deixa de ter uma parábola e passa a ter uma reta, então a não pode ser nulo, logo só nos resta b = 0 . Agora ficamos com:

v = a x 2 + c

Conhecemos duas condições:

x = 0 ; v = v e n t r a d a

x = L ; v = v s a í d a

Vamos substituir essas condições na equação geral:

v s a í d a = a L 2 + c

v e n t r a d a = c

Achamos quem é o c ! Vamos substituir em v s a í d a :

v s a í d a = a L 2 + v e n t r a d a

Podemos isolar o a :

a = v s a í d a - v e n t r a d a L 2

Agora que conhecemos a   e c podemos substituir na equação geral:

v = v s a í d a - v e n t r a d a L 2 x 2 + v e n t r a d a

Tcharaaaam! Achamos a expressão de velocidade!!!

Resposta

v = v s a í d a - v e n t r a d a L 2 x 2 + v e n t r a d a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o filme líquido sendo drenado na Figura P4.36, quais são as condições de contorno apropriadas (a) no fundo em y = 0 e (b) na superfície em y = h ?
Vamos analisar a expansão brusca do escoamento no tubo da Figura P3.59, usando as equações completas da continuidade e de Navier-Stokes. Quais são as condições de contorno apropriadas para lidar com e
Vamos analisar o escoamento oscilatório no tubo U da Figura P3.96, usando as condições completas de continuidade e de Navier-Stokes. Quais são as condições de contorno adequadas para resolver este pro
Fluido de um grande reservatório à temperatura T 0 escoa por um tubo circular de raio R. As paredes do tubo estão envolvidas por uma resistência elétrica que fornece calor para o fluido a uma taxa q w
Modifique a análise da Figura 4.13 para encontrar a velocidade u θ quando o cilindro interno é fixo e o cilindro externo gira a uma velocidade angular Ω 0 . Pode essa solução ser somada à Equação (4.1