Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 81
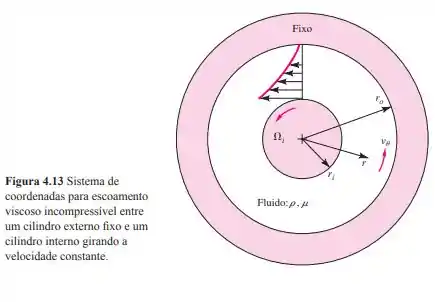
Modifique a análise da Figura 4.13 para encontrar a velocidade quando o cilindro interno é fixo e o cilindro externo gira a uma velocidade angular . Pode essa solução ser somada à Equação (4.140) para representar o escoamento que ocorre quando ambos os cilindros, interno e externo, giram? Explique a sua conclusão.
Passo 1
Bora pra mais uma!
Da solução equação 4.139: , vamos aplicar novas condições de contorno:
Resolvendo este sistema, obtemos:
Daí obtemos:
Resposta
A velocidade quando o cilindro interno é fixo e o cilindro externo gira a uma velocidade angular é:
Esta solução pode de fato ser adicionada à solução da equação 4.140, porque a aceleração convectiva é zero, logo, a equação de Navier-Stokes é linear.
Exercícios de Livros Relacionados
Defina campo de escoamento em regime permanente no sistema de referência euleriano. Em tal escoamento permanente é possível que uma partícula de fluido sofra uma aceleração diferente de zero?
Uma sonda estática de Pitot com frequência pode ser vista na parle inferior de um avião (Figura). À medida que o avião voa, a sonda mede a velocidade relativa do vento. Essa é uma medição lagrangiana
Uma sonda fixa é colocada em um escoamento de fluido e mede a pressão e a temperatura como funções do tempo em determinado local do escoamento (Figura). Essa é umamedição lagrangiana ou euleriana? Exp
Considere o seguinte campo de velocidade em regime permanente e bidimensional: V → = u ,v = 0,5 + 1,2 x i → + ( - 2,0 - 1,2 y ) j → Existe algum ponto de estagnação nesse campo de escoamento? Se exist
Considere o seguinte campo de velocidade estacionário e bidimensional: V → = u ,v = a 2 - b - c x 2 i → + ( - 2 c b y + 2 c 2 x y ) j → Existe algum ponto de estagnação nesse campo de escoamento?Se ex