Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 53

Considere o escoamento incompressível na entrada de um tubo, como mostrado a seguir. O escoamento na entrada é uniforme, u 1 = U 0 . O escoamento na seção 2 já está desenvolvido. Encontre a força de arrasto na parede, F, em função de ( p 1 , p 2 , ρ , U 0 , R ) , se o escoamento na seção 2 for:

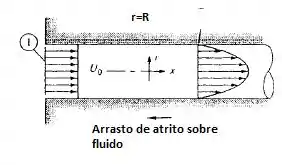
  1. Laminar u 2 = u m á x 1 - r 2 R 2
  2. Turbulento u 2 = u m á x 1 - r R 1 7

Passo 1

Olá, meus abiguinss! Tudo bem? Vamos para mais um desafio de mecânica dos fluidos!!!

Primeiro de tudo vamos estabelecer um volume de controle dentro do nosso domínio, de estudo, beleza?

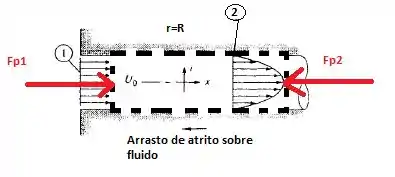
Considerando que nosso fluido está contido dentro de um tubo de diâmetro consideravelmente pequeno tal que a pressão em r= R e r=-R sejam iguais, temos que as forças de pressão também irão se cancelar nesse sentido. Porém para o eixo x, temos que:

∑ F x = F P 1 - F P 2 - F a r r a s t o + m ˙ e u e - m ˙ s u s = 0

∑ F x = p 1 A 1 - p 2 A 2 - F a r r a s t o + U 0 ρ π R 2 U 0 - ∫ 0 R ρ u 2 2 π r d r u 2 = 0

Note que não precisamos estabelecer a relação entre u m á x e U 0 pela integração, porque o resultado para os dois perfis já foi dado pelo livro durante o texto corrido.

Sabendo que as áreas que as forças de pressão são iguais, temos que:

p 1 - p 2 π R 2 - F a r r a s t o = ∫ 0 R ρ u 2 2 π r d r u 2 - U 0 ρ π R 2 U 0 = ρ π R 2 U 0 2 β 2 - 1

Passo 2

A gente aqui só acrescentou o fator de fluxo de momento de forma apropriada, que é o nosso fator β . Para o caso laminar, sabe-se que β = 4 3 e para o caso turbulento β pode ser aproximado ao valor de 1,020.

Passo 3

  1. Laminar: F a r r a s t o = p 1 - p 2 π R 2 - ρ π R 2 U 0 2 4 3 - 1 = p 1 - p 2 π R 2 - 1 3 ρ π R 2 U 0 2
  2. Turbulento: F a r r a s t o = p 1 - p 2 π R 2 - 0,02 ρ π R 2 U 0 2

Resposta

  1. p 1 - p 2 π R 2 - 1 3 ρ π R 2 U 0 2
  2. Turbulento: F a r r a s t o = p 1 - p 2 π R 2 - 0,02 ρ π R 2 U 0 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cotovelo redutor é usado para defletir o escoamento da água a uma taxa de 30k g / s em um tubo horizontal para cima de um ângulo θ = 45 ° da direção do escoamento enquanto a acelera. O cotovelo des
Um jato d’água horizontal com velocidade constante V é imposto normalmente a uma placa plana vertical e se espalha nas laterais no plano vertical. A placa se move na direção da entrada do jato d’água
A água acelerada por um bocal até 15m / s atinge a superfície traseira vertical de um carrinho que se move horizontalmente a uma velocidade constante de 5m / s na direção do escoamento. A vazão em mas
Um cotovelo de 90 ° é usado para direcionar o escoamento da água a uma taxa de 25k g / s em um tubo horizontal para cima. O diâmetro de todo o cotovelo é de 10c m . O cotovelo descarrega água na atmos
Um jato d’água horizontal a velocidade constante de um bocal fixo é imposto normalmente a uma placa plana vertical que é mantida em um trilho quase sem atrito. À medida que o jato d’água atinge a plac