Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 30

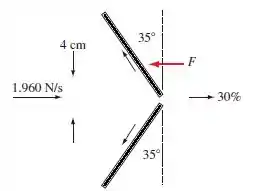
Um jato de água bidimensional em regime permanente, com espessura de 4 cm e uma vazão em peso de 1960 N/s, colide com uma barreira em ângulo como mostrado abaixo. A pressão e a velocidade da água são constantes em todos os pontos. Trinta por cento do jato passa através de uma abertura. O restante se divide simetricamente ao longo da barreira. Calcule a força horizontal F necessária para segurar a barreira por unidade de espessura na direção normal ao papel.

Passo 1

Bem, aqui eu te recomendo a lembrar da lei de Newton para analisarmos a questão das forças!

Para um sistema em equilíbrio as forças somadas sobre um corpo devem resultar em 0, certo? Como temos uma força F sendo aplicada na direção decrescendo do eixo X, vamos ter que:

∑ F x = 0

Isso é o mesmo que dizer que as duas forças que estão atuando no nosso sistema acima devem ser iguais em módulo, mas com sinais opostos.

F = m ˙ e u e

Passo 2

Agora vamos lembrar do seguinte:

m ˙ e = ρ A V = 979   x   0,04   x   1   x   u

Note que vamos precisar então encontrar qual é essa velocidade, beleza?

A vazão foi dada em peso/s, logo se quisermos encontrar a vazão em kg/s, precisamos dividir pela gravidade e assim obtemos que a vazão mássica será 1960/10 = 196 kg/s.

Logo, a velocidade é: u = 196 979 x 0,04 x 1 = 5   m / s

Passo 3

Pelo balanço de força, temos então que:

F = m ˙ e u e

Precisamos decompor nosso vetor velocidade de tal forma que pelo desenho é observado que u e , x = u e cos ⁡ θ 2 - 1 . Além disso, apenas 30% do fluido passa pelo orifício, isso indica que 70% da água fica retido internamente gerando uma força nas paredes, certo?

u e , x = 0,7 u e cos ⁡ θ 2 - 1

F = m ˙ e 0,7 u e cos ⁡ θ 2 - 1 = 196 x 0,7 x 5 x ( cos ⁡ 35 ° 2 - 1 = 657 ,   75   N

Resposta

F = 657 ,   75   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque da figura abaixo permanece em nível constante. O escoamento na calha tem uma seção transversal quadrada e é bidimensional, obedecendo à equação v = 3 y 2 . Sabendo que o tanque B tem 1m 3 e é
O esquema a seguir corresponde à seção longitudinal de um canal de 25c m de largura. Admitindo escoamento bidimensional e sendo o diagrama de velocidades dado por v = 30 y - y 2 ( ye mc m ; ve mc m /
No sistema da figura, A 3 = 0,5m 2 , ρ 3 = 0,4k g / m 3 e os fluidos são gases. Dados: Seção ( 1 ) : v = 4 1 - r R 2 ; Q 1 = 2m 3 / s ; ρ 1 = 0,6k g / m 3 Seção ( 2 ) : v = 9 1 - r 0,4 ; ρ 2 = 1,2k g
O insuflador de ar da figura gera 16.200m 3 / h na seção ( 0 ) com uma velocidade média de 9,23m / s . Foram medidas as temperaturas nas seções 0 ,( 1 ) e ( 2 ) , sendo, respectivamente, t 0 = 17 ° C
O campo de velocidades de um escoamento bidimensional é dado por v x = 3 + 2 x y + 4 t 2 , v y = x y 2 + 3 t . Determinar os módulos da velocidade e aceleração no ponto 2 ; 1 no instante t = 5s .