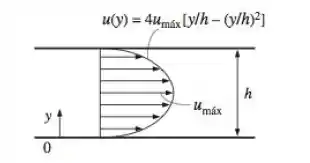
Considere o escoamento laminar de um fluido newtoniano de viscosidade entre duas placas paralelas. O escoamento é unidimensional e o perfil de velocidade é expresso com onde é a coordenada vertical da superfície do fundo, é a distância entre as duas placas e a velocidade máxima do escoamento que ocorre no plano do meio. Desenvolva uma expressão para a força de arrasto exercida em ambas as placas pelo fluido na direção do escoamento por unidade de área das placas.
Passo 1
Bora então!!
Temos um fluido newtoniano, então podemos usar a seguinte expressão:
A questão da pra a gente a expressão do perfil de velocidade:
Onde é a coordenada vertical, é a distância entre as duas placas e a velocidade máxima que vai estar bem no meio, entre as duas placas, poderiamos inclusive dizer que fica em .
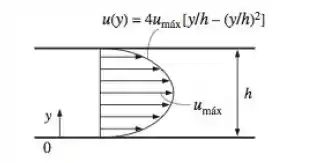
Como a gente pode ver na imagem, a questão já determina o sistema de coordenadas, na placa inferior , o escoamento é unidimensional, então é a unica coordenada que a gente vai ter que se preocupar! Beleza?
A tesão de cisalhamento é dada por:
Bora colocar a mão na massa então?!
Passo 2
A tensão de cisalhamento é dada pela seguinte expressão:
Temos a expressão da velocidade dada no enunciado:
Substituindo:
Agora a gente tira pra fora da derivada, porque é constante:
Agora é só derivar!
Para a placa inferior , então vamos substituir:
Passo 3
A gente achou a tensão de cisalhamento da placa inferior, quando , mas ainda falta achar o para a placa superior.
Mas o que vamos fazer aqui é assumir que existe uma simetria no perfil de velocidade e a tensão de cisalhamento da placa inferior é igual a da placa superior! Mas como sabemos dessa simetria?
A primeira dica é a imagem, que mostra uma parábola, depois o enunciado diz que a velocidade máxima fica no meio das duas placas! E por fim é só observar a expressão da velocidade:
Ela tem a carinha de nada mais nada menos do que uma equação de 2º grau!
Sabendo disso, a questão pede a força de arrasto exercida pelo fluido em ambas as placas, se a gente pensar que é o mesmo fluido que ta exercendo a força tanto na placa de cima, quanto na de baixo, podemos dizer que:
Substituindo:
A questão pede a força de arrasto por unidade de área, então:
Chegamos na nossa resposta!!!