Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 68
Alguns fluidos não newtonianos comportam-se como um plástico de Bingham para o qual o esforço de cisalhamento é expresso como . No caso de escoamento laminar de plástico de Bingham num tubo horizontal de raio , o perfil de velocidade é definido pela expressão onde é a queda de pressão constante ao longo do tubo por unidade de comprimento, é a viscosidade dinâmica, é a distância radial do eixo central e é a tensão de escoamento do plástico de Bingham. Determine:
- a tensão de cisalhamento numa parede do tubo
- a força de arrasto que atua na seção do tubo de comprimento .
Passo 1
Bora entender o nosso enunciado um pouquinho melhor, para isso vamos fazer um esqueminha!
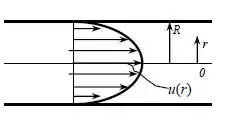
A gente sabe que nesse caso o fluido não é newtoniano, ele é um plástico de Bingham, isso quer dizer que precisamos aplicar uma tensão nele, para ai sim ele começar a sofrer deformação. Então a expressão de tensão cisalhante vai ser essa daqui:
A questão da pra a gente também a expressão de perfil de velocidade:
O raio do tubo é igual a .
Com essas informações a gente já consegue resolver a letra a!
Agora, para a letra b a gente precisa da fórmula para calcular a força de arrasto, que é essa daqui:
Agora, bora colocar a mão na massa??!!
Passo 2
Bora começar a fazer nossa letra a! Que pede a tensão de cisalhamento em uma parede do tubo:
Temos a expressão para a tensão de cisalhamento:
E temos também a expressão de velocidade
Se a gente deriva essa espressão em relação a , a gente pode substituir na expressão de tensão de cisalhamento, certo?
Então bora fazer isso!
A gente quer a tensão de cisalhamento na parede do tubo, quando a gente ta na parede do tubo podemos dizer que , substituindo:
Agora arrumando a casa:
Já podemos substituir na exepressão de tensão de cisalhamento, como tinhamos combinado!
Organizando:
Fechou, temos a resposta da nossa letra a!
Passo 3
Agora vamos de letra b!
Na letra b o que a gente quer é encontrar a força de arrasto que atua na seção do tubo de comprimento . Para isso a gente vai recorrer a seguinte expressão:
O a gente já tem, encontramos na letra a.
Agora a área da secção tranversal do tubo é dada por:
Agora só temos que substituir e na expressão da força de arrasto :
Arrumando:
É isso aêeee! Chegamos na nossa resposta!