Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 18
Considere o modelo simples de lei de potência para um fluido não newtoniano dado pela Eq. 2.16. Estenda a análise da Seção 8.2 para mostrar que o perfil de velocidade da lei de potência para escoamento laminar completamente desenvolvido de um fluido entre placas paralelas separadas pela distância 2h pode ser escrito:
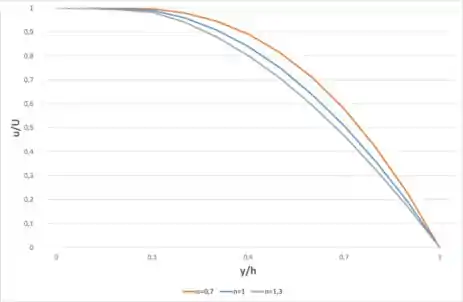
Em que y é a coordenada medida a partir da linha de centro do canal. Trace um gráfico dos perfis versus para e .
Passo 1
Beleza! A primeira coisa que devemos fazer é desenhar o volume de controle para o problema, então, pegando um elemento diferencial qualquer, teremos:
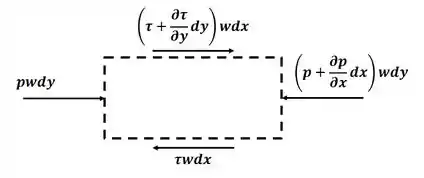
Agora, com o volume de controle, podemos aplicar a equação para o equilíbrio de momento na direção , dada por:
Então, como temos regime permanente, a derivada no tempo será igual a zero, além disso, temos também escoamento totalmente desenvolvido, de forma que a integral sobre a superfície de controle será igual a zero. E, por fim, iremos desprezar as forças de campo na direção , de modo que . Então, a equação acima só irá contar com os termos de força de superfície, de modo que ela se tornará:
Então, eliminando os termos em comum, temos:
Passo 2
Agora, sabemos que é função de y e é função de , então, desse modo sabemos que:
Então, integrando os dois lados da equação em , teremos:
No entanto, sabemos que podemos escrever a tensão de cisalhamento como:
Dessa forma, igualando as duas expressões para a tensão de cisalhamento, temos:
E, para o nosso caso, temos que:
Então, a equação acima se torna:
Passo 3
Agora, integrando a expressão do passo 2 dos dois lados em , temos:
No entanto, nós sabemos que temos velocidade igual a zero na parede, de forma que a condição de contorno será:
Então, substituindo esses valores na expressão anterior, podemos descobrir o valor de :
Então, a equação para a velocidade será:
Colocando o termo em comum em evidência, temos:
Rearranjando a equação para que ela fique igual a dada no enunciado, separando as potências de , temos:
Passo 4
Agora, vamos plotar o gráfico dos perfis versus para e . Então, usando a equação obtida no passo 3, temos:
