Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 20

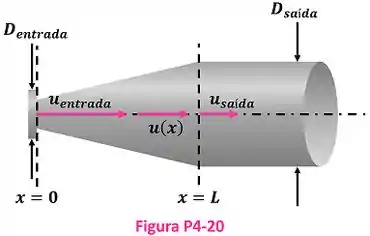
Considere o escoamento permanente do ar através da parte do difusor de um túnel de vento (Figura P4-20). Ao longo do eixo central do difusor, a velocidade do ar diminui de u e n t r a d a para u s a í d a conforme a ilustração. As medições revelam que a velocidade do ar ao longo do eixo central diminui parabolicamente através do difusor. Escreva uma equação para a velocidade do eixo central, u x , com base nos parâmetros dados aqui de x = 0 até x = L .

Passo 1

O exercício pede que a gente calcule a velocidade u do fluido no eixo x central ao longo do difusor. Para fazer esse cálculo, o enunciado informa quatro dados sobre u :

  1. A velocidade u do fluido no eixo central só depende da variável x . O enunciado informa isso, quando diz que:

    2. u = u x

  2. A velocidade do ar ao longo do difusor diminui parabolicamente. Isso significa que:

    3. u x = a ⋅ x 2 + b ⋅ x + c

    onde a , b e c são os coeficientes da parábola que precisamos encontrar.

  3. A velocidade do ar na entrada do difusor x = 0 vale:

    4. u 0 = u e n t r a d a

  4. A velocidade do ar na saída do difusor x = L vale:

u L = u s a í d a

Passo 2

Para facilitar a visualização do perfil de velocidade u ao longo do eixo central, segue abaixo uma imagem do difusor com esse perfil.

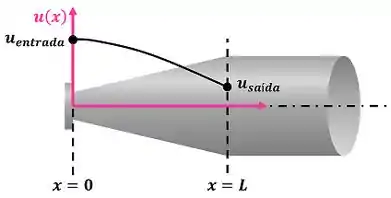
A figura acima com o gráfico parabólico de u x mostra que o valor máximo u x está na entrada do difusor. Isso significa que o vértice da parábola de u (ponto de máximo valor da uma parábola com concavidade para baixo) fica na entrada do difusor x = 0 . Ou seja, o valor da coordenada x do vértice x V é igual a zero.

x V = 0

Além disso, a fórmula do x do vértice x V em função dos coeficientes a , b e c é:

x V = - b 2 ⋅ a

Substituindo o valor de x V nessa f´romula, descobrimos que o coeficiente b vale:

x V = - b 2 ⋅ a       ⟹       0 = - b 2 ⋅ a       ⟹       b = 0

Isso quer dizer que:

u x = a ⋅ x 2 + c

Passo 3

O valor dos coeficientes a e c podem ser determinados, lembrando que:

u 0 = u e n t r a d a

u L = u s a í d a

No entanto, substituindo o valor das coordenadas na equação de u x encontramos:

u x = a ⋅ x 2 + c       ⟹       u 0 = a ⋅ 0 2 + c       ⟹       u 0 = c         ⟹       c = u e n t r a d a

u x = a ⋅ x 2 + c       ⟹       u L = a ⋅ L 2 + c       ⟹       u s a í d a = a ⋅ L 2 + u e n t r a d a

a = u s a í d a - u e n t r a d a L 2

Com esses valores, a equação final de u x vira:

u x = a ⋅ x 2 + c       ⟹       u x = u s a í d a - u e n t r a d a L 2 ⋅ x 2 + u e n t r a d a

Resposta

u x = u s a í d a - u e n t r a d a L 2 ⋅ x 2 + u e n t r a d a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um balão meteorológico é lançado na atmosfera por meteorologistas. Quando o balão atinge uma altitude na qual é neutramente flutuante, ele transmite informações sobre as condiçõesclimáticas para estaç
Qual é a descrição euleriana do movimento dos fluidos? Em que ela difere da descrição lagrangiana?
Defina campo de escoamento em regime permanente no sistema de referência euleriano. Em tal escoamento permanente é possível que uma partícula de fluido sofra uma aceleração diferente de zero?
Uma sonda estática de Pitot com frequência pode ser vista na parle inferior de um avião (Figura). À medida que o avião voa, a sonda mede a velocidade relativa do vento. Essa é uma medição lagrangiana
Uma sonda fixa é colocada em um escoamento de fluido e mede a pressão e a temperatura como funções do tempo em determinado local do escoamento (Figura). Essa é umamedição lagrangiana ou euleriana? Exp