Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 103
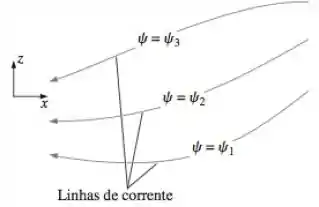
Considere o escoamento permanente, bidimensional, incompressível no plano em vez do plano . Na Figura P9-103 são mostradas curvas com função corrente constante. As componentes de velocidade diferentes de zero são . Defina uma função corrente tal que o escoamento seja da direita para a esquerda no plano quando aumenta na direção .
Passo 1
Fala Galera!!
Nessa questão, nos foi dito que o fluxo é constante, bidimensional e incompressível no plano , também foi dito que o fluxo é da direita para a esquerda no plano quando aumenta na direção .
Passo 2
Assim, temos que pela equação 9-20, podemos dizer que a função corrente para o escoamento da direita para a esquerda no plano quando aumenta na direção pode ser dada da seguinte maneira:
Resposta
Exercícios de Livros Relacionados
Para o campo de velocidade do Problema 9-49, faça o gráfico das linhas de corrente ψ = 0 ,1 ,2 ,3 ,4 ,5 e 6m 2 / s . Considere as constantes a , b e c com os seguintes valores: a = 0,5s - 1 , b = - 1,
Considere o escoamento axissimétrico permanente incompressível ( r ,z ) e u r ,u z para o qual a função corrente é definida por u r = - 1 r ∂ ψ ∂ z e u z = 1 r ∂ ψ ∂ r . Verifique se ψ assim definida
Se a velocidade média no ramo principal do duto do Problema 9-53 for 11,4m / s , calcule a altura h do duto em c m . Obtenha o seu resultado de duas maneiras, mostrando todo o seu trabalho. Você pode
Repita o Problema 9-56 para o caso de uma linha de sumidouros em lugar de uma linha de fontes. Suponha que V ˙ / L seja um valor positivo, mas o escoamento em todos os pontos é na direção oposta.
Considere o escoamento bidimensional permanente, incompressível devido a uma linha de fontes na origem (Figura P9-56). O fluido é criado na origem e se espalha rapidamente em todas as direções no plan