Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 84

Repita o problema 4 - 83 , exceto que a tinta é introduzida de t = 0 a t = 10 s e as linhas de emissão devem ser traçadas em t = 12   s em vez de 10   s .

Passo 1

Fala aí galera, Bora pra mais uma questão de Mecânica dos Fluidos. Primeiramente, Como o fluxo é constante, as linhas, as linhas de fluxo são horizontais. Logo, precisamos integrar a componente de velocidade u em relação ao tempo durante o período especificado. O componente de velocidade horizontal é dada por:

u = 1 2 μ d P d x ( y 2 - h y )

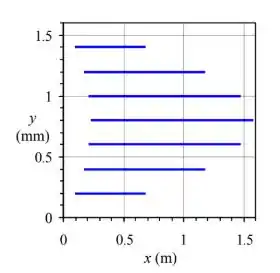
Com isso, temos que no problema anterior, geramos linhas de raíz em t = 10   s . Imagine a tinta na fonte sendo cortada repentinamente naquele momento, mas as linhas de são observadas 2 segundos depois, em t = 12   s . As manchas de tinta não se estendem mais, mas simplesmente se movem na mesma velocidade horizontal por mais 2 segundos. Em cada local y, os x locais da primeira e da última partícula de corante são assim:

x = x i n i c i o + ∫ t 0 t i u   d t = 0 + ∫ 0 10 1 2 μ d P d x y 2 - h y   d t x = 1 2 μ d P d x y 2 - h y 1 2   s                                   ( 2 )

E as partículas finais, são:

x = 1 2 μ d P d x y 2 - h y 12   s                                   ( 3 )

Passo 2

Por fim, substituímos os valores fornecidos de y   e os valores de μ e d P / d x nas Eqs. ( 2 ) e ( 3 ) para calcularmos as posições x final e inicial da primeira e da última partícula de tinta liberada de cada linha. Ao conectarmos os pontos inicial e final para plotar as linhas de listras, temos:

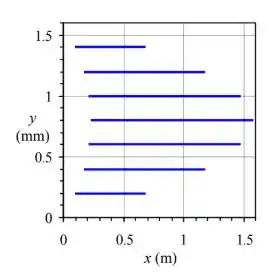
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento de Poiseuille com simetria axial completamente desenvolvido – o escoamento em um tubo redondo de raio R (diâmetro D = 2 R ), com um gradiente de pressão forçado d P / d x movend
Considere o escoamento de Poiseuille com simetria axial do problema 4 - 87 , calcule as taxas de deformação linear nas deireções x e r e calcule a taxa de deformação por cisalhamento ϵ x r . O tensor
Combine seus resultados do problema 4-80 para formar o tensor da taxa de deformação bidimensional ε i j no plano x y ε i j = ε x xε x y ε y x ε y y Os eixos x e y são principais?
Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40° C . Seja h = 1,6m m a altura da lacuna e d P / d x = - 230N / m 3 o gradiente de pressão.
Combine seus resultados do Problema 4 - 88 para formar o tensor taxa de deformação simétrico ϵ y . ϵ i j = ϵ r r ϵ r x ϵ x r ϵ x x Os eixos x e r são principais?