Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 100

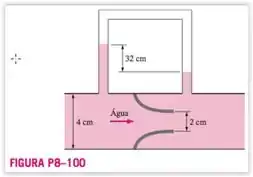
A vazão da água a 20 ° C ( ρ = 998 k g m 3 e   μ = 1,002 × 10 - 3   k g / m ∙ s ) através de um tubo com diâmetro de 4   c m de diâmetro é medida com um medidor de bocal equipado com um manômetro de ar e água invertido. Se o manômetro indicar uma altura diferencial da água de 32   c m , determine a vazão volumétrica da água e a perda de carga causada pelo medidor de bocal.

Passo 1

Bom, nesse problema vamos determinar a vazão volumétrica da água e a perda de carga. Nos atentamos que é um problema de obstrução e para isso temos alguns requisitos.

A vazão é determinada por:

v ˙ = A 0 C d 2 P 1 - P 2 ρ 1 - β 4

Nesse caso, chutamos um valor de coeficiente de descarga do medidor de bico para C d = 0,97 .

Calculamos A 0 que é a área da seção transversal do orifício e β a razão entre o diâmetro do orifício e diâmetro do tubo:

A 0 = π d 2 4 = π 0,02 2 4 = 3,14 × 10 - 4   m 2

β = d D = 2 4 = 0,5

Passo 2

Como temos um manômetro invertido, usamos a pressão manométrica para que possamos calcular C d . Considerando que apenas a densidade varia, logo:

v ˙ = A 0 C d 2 ρ á g u a - ρ a r g h ρ á g u a 1 - β 4

Substituindo os dados:

v ˙ = 3,14 × 10 - 4   m 2 × 0,97 × 2 998 - 1,20 × 9,81 × 0,32 998 1 - 0,5 4 = 0,000788 m 3 s

Agora, vamos calcular a velocidade através da vazão:

V = 4 v ˙ π D 2 = 4 × 0,000788 π ( 0,04 ) 2 = 0,62707 m s

Calculamos o numero de Reynolds:

R e = ρ V D μ = 998 × 0,62707 × 0,04 1,002 × 10 - 3 = 2,498 × 10 4

Passo 3

Tendo os dados, podemos conferir o coeficiente de descarga:

C d = 0,9975 - 6,53 β 0,5 R e 0,5

C d = 0,9975 - 6,53 β 0,5 ( 2,498 × 10 4 ) 0,5 = 0,968 = 0,97

O qual chegou próximo do nosso chute inicial no momento que aproximamos.

Passo 4

Por fim, podemos calcular a perda de carga pela equação de energia. Com a altura z 1 = z 2   , sem bomba nem turbina e considerando α = 1 , temos:

P 1 ρ g + α 1 V 1 2 2 g + z 1 + h b o m b a = P 2 ρ g + α 2 V 2 2 2 g + z 2 + h t u r b i n a + h L

P 1 ρ g + V 1 2 2 g = P 2 ρ g + V 2 2 2 g + h L

Isolamos h L :

h L = P 1 - P 2 ρ g + V 1 2 - V 2 2 2 g

Considerando que temos pressão manométrica:

h L = ρ á g u a - ρ a r g h ρ g + V 1 2 - V 2 2 2 g

Muita atenção que a velocidade no ponto 2 deve ser considerada uma razão entre a área do orifício e o ponto mais o ponto 1 , ou seja:

V 1 2 - V 2 2 = V 1 2 - 4 v ˙ π d 2 4 v ˙ π D 2 2 V 1 2 = V 1 2 - 4 v ˙ π d 2 × π D 2 4 v ˙ 2 V 1 2 = V 1 2 - D d 4 V 1 2

Logo,

h L = h + V 1 2 - D d 4 V 1 2 2 g = 0,01938   m

Prontinho!!

Resposta

v ˙ = 0,000788 m 3 s e h L = 0,01938   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo que transporta óleo a 40 ° C a uma taxa de 3 m 3 s , se divide em dois tubos paralelos feitos de aço comercial que se reconectam a jusante. O tubo A tem 500m de comprimento e diâmetro de 30c m
Um tubo circular de água tem uma expansão abrupta do diâmetro D 1 = 15c m para D 2 = 20c m . A pressão e a velocidade média da água no tubo menor são P 1 = 120k P a e 10m / s , respectivamente, e o es
Em uma usina hidrelétrica a água a 20 ° C é fornecida para a turbina a uma taxa de 0,8m 3 / s através de um tubo de ferro fundido com 200m de comprimento e 0,35m de diâmetro. A diferença de elevação e
No Problema 8 - 112 , o diâmetro do tubo é triplicado para reduzir as perdas do tubo. Determine o aumento percentual na saída de potência liquida como resultado dessa modificação.
A água em uma piscina acima do solo a 20 ° C , com 10m de diâmetro e 2m de altura deve ser esvaziada destampando um tubo plástico horizontal com 3c m de diâmetro e 25m de comprimento anexado à parte i