Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 86
A comporta BC em forma de um quarto de círculo da Figura P2.86 é articulada em C. Encontre a força horizontal P necessária para manter a comporta parada. Despreze o peso da comporta.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.6 do livro, chamada “Forças sobre superfícies curvas”.
Pra entender a questão, dá uma olhada na figura do enunciado. Temos uma comporta no formato de um quarto de círculo, com um raio de e uma largura (imagina isso como uma terceira coordenada que “entra” dentro do papel) não especificada que vamos chamar de .
Essa comporta tem um ponto articulado , que não pode se mover. Devemos descobrir, então, a força necessária que seja aplicada na barragem para que o ponto não se mova, desprezando o peso da comporta.
Para isso, devemos descobrir as componentes horizontal e vertical da força hidrostática agindo, respectivamente e , como demonstra a imagem abaixo:
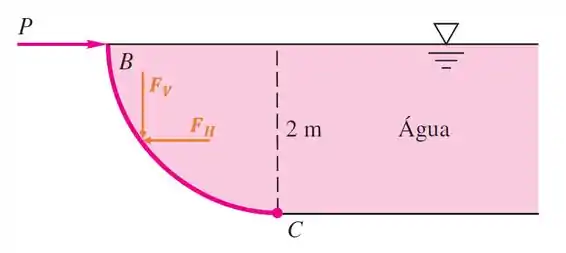
Nos passos seguintes, vamos descobrir como calcular cada uma das componentes das forças hidrostáticas, suas linhas de aplicação e, no fim, fazer um balanço de momento para descobrir qual a força .
Então, vamo lá resolver essa questão juntos!
Passo 2
Primeiro, vamos calcular a componente horizontal . Para isso, devemos imaginar uma projeção em um ângulo de 90° com relação à direção dessa força, como na figura abaixo:
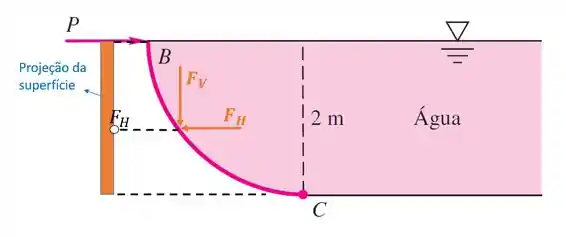
Observe que essa projeção é na verdade um retângulo, de base e altura . Sabendo disso, podemos definir a equação para calcular a componente vertical da força hidrostática:
Sendo: o peso específico, que para água à temperatura ambiente é 9790 ; a distância do centro de massa com relação à superfície livre, que para um retângulo é metade da altura do retângulo; e a área do retângulo projetado.
Como não há definição do valor de no enunciado, vãos assumi-lo como sendo .
Dessa forma, temos:
Além disso, devemos calcular a linha de aplicação da componente horizontal da força com relação ao centroide, que podemos chamar de . Pra isso, vamos utilizar a equação abaixo:
Sendo: o ângulo entre a projeção e a horizontal, que, por definição, é 90°; e o momento de inércia para essa direção.
O momento de inércia de um retângulo, o próprio livro define na página 92 como :
Sendo: a largura do retângulo , ou seja, ; e a altura do retângulo, que nesse caso é . Logo:
Calculando então a linha de aplicação com relação ao centroide, temos:
Para calcular a linha de aplicação com relação a (que vamos chamar aqui simplesmente de ) devemos simplesmente subtrair da distância de com relação à superfície livre ():
Passo 3
Agora vamos calcular a componente vertical . Nesse caso, ela poderá ser calculada a partir do peso da água acima da barragem e é dada pela equação:
Sendo o volume da água acima da comporta no formato de um quarto de círculo. Sendo assim, temos:
Pra calcular a linha de aplicação para a componente vertical, basta ir novamente na página 92 e usar a mesma distância do centroide para um semi-círculo. Ou seja, a linha de aplicação pode ser calculada como:
Passo 4
E pra finalizar a questão, iremos fazer um balanço de momento em sentido horário para o ponto , considerando que o sistema deve estar em equilíbrio para não se mover (ou seja, o somatório de momento deve ser zero):
Sendo a distância de aplicação da força com relação ao ponto , que é de , como mostra a figura. Dessa forma:
Pronto, resolvemos a questão juntos!
Resposta
A força necessária para manter a comporta parada é