Um secador de grãos é constituído por um longo duto semicircular com raio . Metade da superfície da base é ocupada por uma placa eletricamente aquecida, com emissividade , enquanto a outra metade suporta os grãos a serem secos, que têm uma emissividade de . Em um processo de secagem em batelada, no qual a temperatura dos grãos é de , de água devem ser removidos por metro de comprimento do duto em um período de 1 hora.

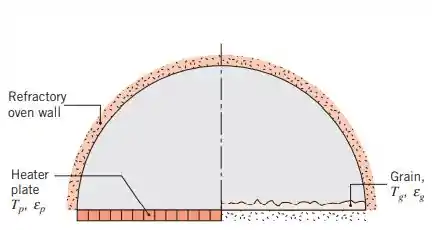
(a) Desprezando a transferência de calor por convecção, determine a temperatura que a placa aquecedora deve ter.

(b) Se o vapor de água é removido do duto pelo escoamento de ar seco, qual é o valor do coeficiente de transferência de massa que deve ser mantido pelo escoamento?

(c) Se o ar estiver a , a hipótese de convecção desprezível se justifica?

Letra a)

O problema nos diz que a transferência de calor por convecção é desprezível, assim, somente a radiação está fornecendo calor suficiente para evaporar a água:

Essa transferência de calor por radiação também pode ser dada na seguinte forma:

Igualando as nossas equações:

Onde:

Inferindo os fatores de forma:

Substituindo os dados na nossa equação:

Resolvendo essa equação, obtemos:

Letra b)

Calculando o valor do coeficiente de transferência de massa .

Sabemos que a vazão mássica de evaporação é dada por:

Abrindo, rearranjando e isolando nessa equação:

Substituindo os dados:

Letra c)

Aqui, devemos confirmar se com o ar estiver a , a hipótese de convecção desprezível se justifica.

Para a convecção ser desprezível:

Sabemos que:

Já o calor convectivo é dado por:

Não temos o coeficiente convectivo, mas podemos calculá-lo!

Sendo:

Temos:

Substituindo os dados:

Assim, nosso calor convectivo é:

Como:

Podemos considerar a convecção desprezível!