Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 13.Problemas - Ex. 92

Silício sólido puro é produzido a partir de material fundido, como por exemplo, no Problema 1.37. Silício sólido é semitransparente e a distribuição do coeficiente de absorção espectral para o silício puro pode ser aproximada por

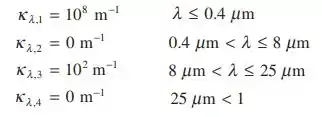
(a) Determine o coeficiente de absorção total, definido como

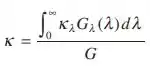
para a irradiação a partir da vizinhança a uma temperatura igual ao ponto de fusão do silício.

(b) Estime a transmissividade total, a absortividade total e a emissividade total de uma lâmina de silício sólido, com L = 140   μ m de espessura, no seu ponto de fusão.

Passo 1

E aí, tudo bem?

Bora resolver essa questão juntos?

Vem comigo!

Letra a)

O problema já nos forneceu a seguinte equação:

k = ∫ 0 ∞ k λ G λ d λ G

Modificando essa equação:

k ≅ ∫ 0 ∞ k λ λ E λ , b ( λ , T f u s ã o ) d λ ∫ 0 ∞ E λ , b ( λ , T f u s ã o ) d λ

Com:

k ≅ k λ , 1 F 0 → 0,4   μ m ⋅ T f u s ã o + k λ , 2 F 0 , 4 → 8   μ m ⋅ T f u s ã o + k λ , 3 F 8 → 25   μ m ⋅ T f u s ã o + k λ , 4 F 25   μ m ⋅ T f u s ã o

Pela Tabela A.1, temos que a temperatura de fusão do silício é 1685   K .

Assim, pela Tabela 12.2, obtemos:

F 0 → 0,4   μ m ⋅ 1685   K = 0

F 0,4   μ m ⋅ 1685   K → 8   μ m ⋅ 1685   K = 0,955

F 8   μ m ⋅ 1685   K → 15   μ m ⋅ 1685   K = 0,998 - 0,955 = 0,043

F 15   μ m ⋅ 1685   K = 1 - 0,998 = 0,002

Substituindo na equação de k :

k ≅ 10 8 ⋅ 0 + 0 ⋅ 0,955 + 10 2 ⋅ 0,043 + 0 ⋅ 0,002

k ≅ 4,3   m - 1

Vamos para a letra b!

Passo 2

Letra b)

Aqui, queremos a transmissividade total, a absortividade total e a emissividade total de uma lâmina de silício sólido.

Calculado a transmissividade total:

k ≅ k λ , 1 F 0 → 0,4   μ m ⋅ T f u s ã o + k λ , 2 F 0,4 → 8   μ m ⋅ T f u s ã o + k λ , 3 F 8 → 25   μ m ⋅ T f u s ã o + k λ , 4 F 25   μ m ⋅ T f u s ã o

τ ≅ τ λ , 1 F 0 → 0,4   μ m ⋅ T f u s ã o + τ λ , 2 F 0,4 → 8   μ m ⋅ T f u s ã o + τ λ , 3 F 8 → 25   μ m ⋅ T f u s ã o + τ λ , 4 F 25   μ m ⋅ T f u s ã o

Como os termos de F são os mesmos do Passo e, devemos calcular os τ pela seguinte fórmula:

τ λ = e - k λ L

Assim, temos:

τ = 0 + e - 0 ⋅ 140 × 10 - 6 ⋅ 0,955 + e - 1 0 2 ⋅ 1 4 0 × 10 - 6 ⋅ 0 , 043 + e - 0 ⋅ 1 40 × 10 - 6 ⋅ 0 , 002

τ = 0,999

Calculando a absortividade total:

α = 1 - τ = 1 - 0,999

α = 0,001

Obtendo a emissividade total:

α = ε = 0,001

Até a próxima questão!

Resposta

a )   k ≅ 4,3   m - 1

b )   τ = 0,999 ;   α = ε = 0,001 ;  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13.56 Determine as temperaturas em regime estacionário de duas barreiras de radiação colocadas em um espaço onde há vácuo entre dois planos infinitos a temperaturas de 600 e 325 K. Todas as superfície
A extremidade de um tanque cilíndrico no espaço, que contém um propelente criogênico líquido, deve ser protegida da radiação externa (solar) pela colocação de uma fina barreira metálica em frente ao t
13.52 Um dispositivo eletrônico dissipando 50 W é fixado à superfície interna de um recipiente cúbico isotérmico, que tem 120 mm de lado. O recipiente está posicionado na maior área de serviço do ônib
Uma barreira de radiação difusa e cinza, com 60 mm de diâmetro e emissividades ε2,i = 0,01 e ε2,e = 0,1 nas superfícies interna e externa, respectivamente, é concêntrica a um longo tubo que transporta
Um fluido criogênico escoa por um tubo com 20 mm de diâmetro, cuja superfície externa é difusa e cinza, com uma emissividade de 0,02 e uma temperatura de 77 K. Esse tubo é concêntrico a um tubo maior,