Uma operação de colagem utiliza um laser para fornecer um fluxo de calor constante, , através da superfície superior de uma fina película de plástico cuja superfície inferior é adesiva e deve ser fixada a uma fita de metal, conforme mostrado na figura. A fita de metal possui uma espessura d = 1,25 mm e sua largura é grande em relação à da película de plástico. As
propriedades termofísicas da fita são . A resistência térmica da película de plástico, com largura , é desprezível. Nas superfícies superior e inferior da fita (incluindo a película de plástico) há convecção com ar a 25°C e um coeficiente convectivo de . A fita e a película são muito grandes na direção normal à página. Admita que as laterais da fita de metal se encontram à temperatura do ar ().
- Deduza uma expressão para a distribuição de temperaturas na porção da fita de aço com a película de plástico .
- Se o fluxo de calor fornecido pelo laser for de , determine a temperatura no centro (x = 0) e nas laterais da película de plástico.
- Represente graficamente a distribuição de temperaturas para toda a fita e aponte as suas principais características.

Passo 1
Vamos que vamos galerinhaa??
Antes de qualquer coisa nós precisamos dar uma olhadinha mais de perto para o balanço de energia em um volume de controle diferencial, ok?
Então, se pegarmos um pedacinho da placa de comprimento :
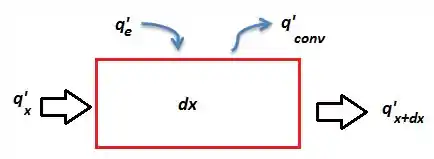
Quando nós fazemos o balanço de energia teremos que o calor sendo adicionado ao volume, e , e saindo do volume de controle, e Então:
Já vimos das questões anteriores que quando nós temos este balanço a equação diferencial que governa a distribuição de temperatura será dada por:
Se nós assumirmos que:
Então:
A fórmula fica:
Quando nós temos uma equação diferencial de segunda ordem com coeficientes constantes a solução é dada pela forma:
O arranjo de filme plástico-tira pode ser modelado como uma aleta infinita de seção transversal uniforme, uma parte da qual é exposta ao fluxo de calor do laser na superfície superior, então:
Beleza, na letra (a) nós queremos deduzir uma expressão para a distribuição de temperaturas na porção da fita de aço com a película de plástico , certo?
Olhando a figura do nosso problema na porção de interesse:

Na primeira parte da fita de metal, onde ela está recebendo calor nós teremos que:
Na outra parte a fita não está recebendo calor, então:
Agora nós precisamos aplicar as condições de contorno certo?
No primeiro intervalo analisado não há variação da temperatura com relação à distância, já que estão sob as mesmas condições. Então, quando teremos .
Derivando:
Substituindo a condição:
Já achamos uma informação importante, ok?
Vamos ir lá pra frente e aplicar a última condição de contorno !! Quando a temperatura deverá ser igual à temperatura ambiente, portanto :
No ponto a temperatura deve ser igual usando tanto a primeira relação, para , quanto para a segunda,
Consequentemente:
Substituindo
Achando e, consequentemente,
Agora é só achar o
Reorganizando:
E depois de tanta luta nós vamos substituir nossas constantes na solução:
Mas ainda precisamos da letra (b), certo?
Passo 2
Na letra (b) nós vamos usar a equação que acabamos de achar:
Antes de calcular qualquer coisa nós precisamos de achar M e m, ok?
Se:
Sabemos que:
Então:
Quando
Sabendo que:
Em Celsius:
Quando
Sabendo que:
Em Celsius:
Passo 3
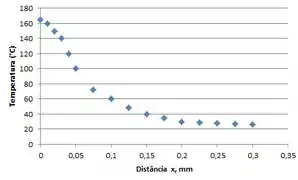
Bom galerinha, para plotar a temperatura versus a distância nós vamos ter que nos atentar que até a distância , 0,02 m, nós usamos , certo?
E a partir daí nós usaremos a , não é?
E com isso é só nos lançarmos os dados no gráfico e terminar nossa questão gigantona:

Bem cabulosa, mas de um jeito legal !! Eu sei que vocês também gostaram !!