Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 92
Reconsidere o Prob. 2-91. Usando a relação obtida para a variação da temperatura na esfera, trace a temperatura como função do raio no intervalo de a . Trace também a temperatura no centro da esfera como função da condutividade térmica no intervalo de a . Discuta os resultados obtidos
Passo 1
O nosso primeiro passo é relembrar a distribuição de temperatura na questão anterior. Com isto, temos:
Vamos começar analisando a variação da temperatura em função do raio. Desta forma, vamos substituir os valores das constantes em relação a questão anterior. Com isto, obtemos a seguinte função:
Plotando o gráfico desta função, temos:
Este resultado era esperado, visto que a temperatura máxima ocorre no centro da esfera, e a mínima na sua superfície.
Passo 2
Para obtermos a temperatura no centro da esfera como função da condutividade térmica, basta fazermos uma variável e na função descrita no Passo 1. Com isto, temos:
Plotando o gráfico desta função, temos:
À medida que aumentamos a condutividade térmica, aumenta a capacidade da esfera de conduzir calor. Consequentemente, a esfera dissipa calor mais facilmente. É por causa disto que a temperatura no centro diminui à medida que aumentamos a condutividade, pois conseguimos dissipar calor mais facilmente.
Resposta
Em relação a variação de temperatura como função do raio, temos:
Este resultado era esperado, visto que a temperatura máxima ocorre no centro da esfera, e a mínima na sua superfície.
Já em relação a condutividade térmica constante, temos:
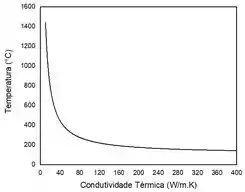
O aumento da condutividade térmica implica no aumento da capacidade da esfera de conduzir calor. Consequentemente, diminui-se a sua temperatura no centro.