Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 85
Reconsidere o Prob. 2-84. Usando a relação obtida para a variação da temperatura no fio, trace a temperatura no eixo central do fio como função da geração de calor no intervalo de a e discuta os resultados. Use EES (ou outro programa).
Passo 1
O nosso primeiro passo é relembrar a distribuição de temperatura na questão anterior. Com isto, temos:
Contudo, como queremos discutir a variação em função de no eixo central do fio , a nossa função na verdade é:
Agora sim, a nossa função está correta! Vamos substituir os valores numéricos das constantes do nosso problema. Com isto, temos:
Vamos aplicar um fator de correção a nossa função, pois o termo é escrito em termos de e não . Portanto,
Agora sim, já podemos partir para no nosso software!
Passo 2
Agora, vamos aplicar a equação determinar acima e observar como varia a temperatura na região central à medida que aumentamos a taxa de geração de calor. Com isto, temos:
Este gráfico nos mostra que o comportamento é linear. O aumento da taxa de geração implica no aumento da temperatura. Este resultado era esperado. Bastava observar que a função temperatura é uma função afim!
Resposta
O gráfico é:
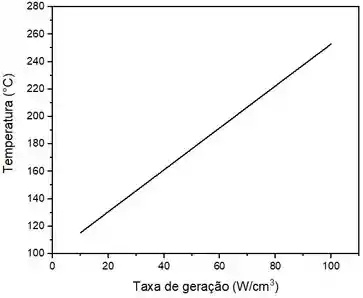
À medida em que aumentamos a taxa de geração, a temperatura aumenta. Este resultado é esperado, pois a função que descreve a temperatura no centro do fio é uma função afim.