Considere uma placa opaca horizontal bem isolada nas bordas e na superfície inferior. A placa é uniformemente irradiada de cima enquanto o ar a 300 K flui sobre a superfície, fornecendo um coeficiente de transferência de calor uniforme por convecção de 40 W/m2.K. Sob condições de estado permanente, a superfície tem radiosidade de 4.000 W/m2, e a temperatura da placa é uniformemente mantida a 350 K. Se a absortividade total da placa é 0,40, determine (a) a irradiação na placa, (b) a refletividade total da placa, (c) o poder emissivo da placa e (d) a emissividade total da placa.
Passo 1
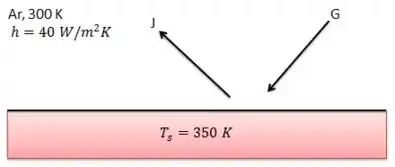
Temos uma placa opaca que recebe irradiação solar. Também sabemos que a placa tem uma temperatura , tem absortividade e emite radiosidade . O ar ao redor da placa tem temperatura e coeficiente convectivo . O exercício nos pede para determinar a irradiação solar , a refletividade da placa (), a radiação emitida pela placa e, a emissividade da placa. Tudo bem? Vamos lá!!!
Passo 2
Nosso primeiro passo é determinar a irradiação que atinge a placa. O enunciado nos diz que estamos em regime permanente. Então, a energia que placa recebe deve ser igual à energia que ela perde. Certo?
A placa só recebe energia por irradiação. Então:
A placa perde energia pela radiosidade e por convecção com ar externo. Ou seja:
Igualando as perdas e ganho de energia:
Pronto. Agora que já encontramos a irradiação, vamos ao próximo ponto pedido pelo exercício.
Temos que determinar a refletividade da placa. Para isso vamos usar a seguinte relação:
Que é válida para qualquer corpo. Já temos a absortividade e sabemos que a placa é opaca, ou seja, não transmite radiação (. Substituindo a absortividade e a transmissividade:
Passo 3
Nosso próximo passo é determinar o poder emissivo da placa. A radiosidade é a soma do poder emissivo e da radiação refletida pela placa:
Já recebemos a radiosidade no enunciado e também já calculamos a refletividade e a irradiação que atinge a placa. Então, podemos usar esta relação para obter o poder emissivo.
Nosso último passo é utilizar este valor de radiação emitida para obter a emissividade média da placa.
Resposta
(a) .
(b) .
(c) .
(d) .