Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 82
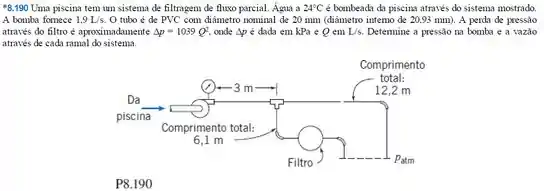
Considere o sistema de filtragem de piscina do Problema 8.190. Considere também que o tubo usado é de PVC, com diâmetro nominal de 20 mm (plástico liso). Especifique a velocidade e o diâmetro do rotor e estime a eficiência de uma bomba adequada.
Passo 1
Beleza! Vamos começar o exercício aplicando o equilíbrio de energia para o sistema entre a saída da bomba (ponto 1) e a bifurcação (ponto 2), então, temos:
Nesse caso, como as dimensões do tubo permanecem constantes, e a vazão também não muda, então temos . Nesse exercício, também não temos diferença entre as cotas e , dessa forma a equação se torna:
E, sabemos que a perda de carga, contendo perdas distribuídas e localizadas, pode ser escrita como:
Como já temos a vazão e o diâmetro da tubulação, vamos calcular a velocidade do sistema:
Passo 2
Agora com a velocidade fornecida no enunciado, conseguimos encontrar o número de Reynolds, para isso, vamos pegar alguns dados da Tabela A.7 do livro:
Então, Reynolds será:
Agora, para encontrar o fator de atrito, precisamos primeiro pegar o dado referente à rugosidade da tubulação, que se encontra na tabela a seguir presente no capítulo 8:
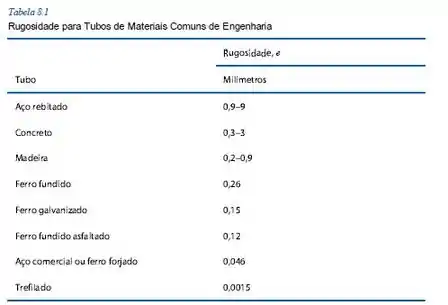
Nesse caso, não temos PVC na tabela, mas como o enunciado disse que temos um plástico liso, então vamos considerar . Então agora podemos usar a equação de Colebrook e descobrir o valor do fator de atrito:
Substituindo os valores conhecidos (lembrando que só conseguimos resolver essa equação com o auxílio de uma calculadora), temos:
Passo 3
Agora vamos voltar à equação do equilíbrio de energia do passo 1:
E substituir a expressão encontrada para a perda de carga no passo 1:
Agora precisamos recorrer às tabelas 8.2 e 8.4 apresentadas no livro e o diagrama para contração/expansão para encontrar os coeficientes de perda:
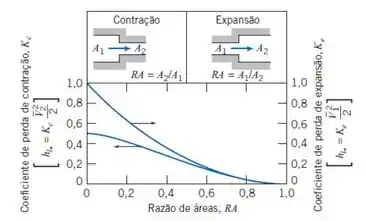
Só que, nesse exercício e para esse trecho não temos acessórios e nem perdas localizadas, dessa forma, temos:
Passo 4
Agora que temos todos os dados, podemos substituir os valores conhecidos na equação de energia do passo 3, então:
Passo 5
Agora, sabendo que independente do caminho percorrido pelo fluido após se separar, ambos irão descarregar na atmosfera, e como eles estão a mesma pressão , então a queda de pressão nos dois trechos deve ser igual.
Onde 3 indica o caminho do filtro e 4 o outro caminho. Então, a equação da energia para o caminhdo do filtro iria se resumir em:
Escrevendo em função da vazão, temos:
E, da mesma forma, para o trecho 4, temos:
Escrevendo em função da vazão, temos:
Igualando as duas expressões para , temos:
No entanto, sabemos que a vazão que vem da bomba se divide nos caminhos 3 e 4, de forma que:
Substituindo o valor de dado no enunciado e a expressão para encontrada, temos:
E então, será:
E a queda de pressão nesse trecho será:
Dessa forma, a altura de carga da bomba será:
Passo 6
Então, para essa altura de carga e para a vazão de , de acordo com o diagrama de seleção de bombas a seguir:
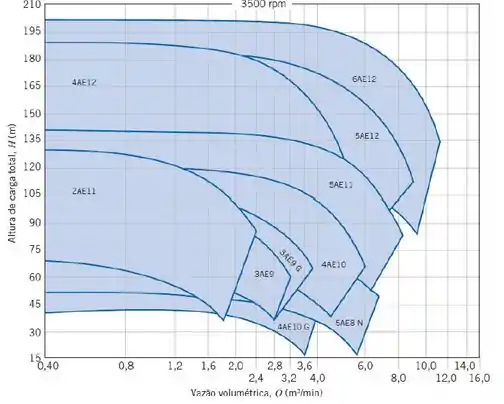
Não temos nenhuma bomba que atende a essas especificações, devido a baixa altura de carga. Então calculando a velocidade específica da bomba assumindo uma rotação , temos:
Obs: com os diagramas fornecidos no apêndice D do livro, também não temos como encontrar um diâmetro para o rotor, já que não conseguimos encontrar um modelo de bomba adequado.
Agora iremos recorrer ao diagrama a seguir para encontrar a eficiência:
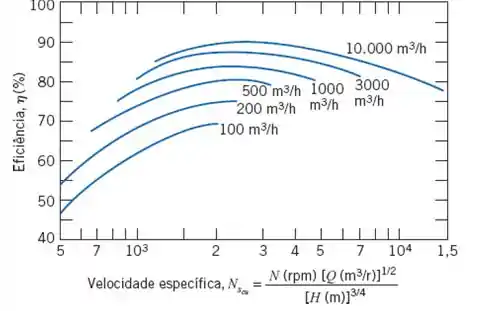
No entanto, ele apresenta a velocidade específica no sistema americano, e conforme vimos no Exemplo 10.2 dessa seção, para converter o valor no sistema internacional para o sistema americano, basta fazer:
Então, através do gráfico, obtemos uma eficiência: