Considere o sótão de uma casa localizada em um local de clima quente. O piso do sótão é caracterizado por uma largura L 1 = 8m , enquanto o telhado faz um ângulo de θ = 30 ° a partir da direção horizontal, como mostrado na figura. O proprietário quer reduzir a carga térmica para a casa através da cola de um filme de alumínio brilhante ( ε f = 0,07 ) sobre as superfícies do espaço do sótão. 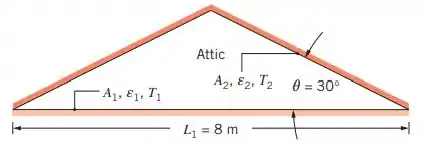Antes da instalação do filme, as superfícies tinham uma emissividade de ε o = 0 , 90 .(a) Considere a instalação somente na superfície inferior do telhado do sótão. Determine a razão entre as transferências de calor radiantes após e antes da instalação do filme.(b) Determine a razão entre as transferências de calor radiantes após e antes da instalação se o filme for instalado somente sobre o piso do sótão.(c) Determine a razão entre as transferências de calor radiantes se o filme for instalado sobre o piso do sótão e na parte inferior do telhado.

a )R = 0,096 b )R = 0,084 c )R = 0,047

Enunciado

Opa, beleza?

Vem comigo resolver essa questão!

Bora lá!

Começamos o nosso problema obtendo a equação de transferência de calor radiante, que é dada da seguinte forma:

Utilizando a regra da soma:

Sendo a superfície 1 plana, não pode se auto incidir radiação, então:

Sobrando:

Não conhecemos o comprimento do sótão, considerando um comprimento unitário para calcularmos e :

Agora, vamos obter o que o problema realmente deseja!

Considerando antes da instalação, temos:

Substituindo os dados na equação de transferência de calor radiante:

Assim, temos que a razão entre as transferências de calor radiante pode ser baseada na seguinte equação:

Agora, só precisamos substituir e para cada caso proposto!

Letra a)

Com:

Temos:

Letra b)

Com:

Temos:

Letra c)

Com:

Temos:

Viu como foi de boa?

Te espero na próxima questão!