Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 28

Determine as temperaturas das superfícies de 1 a 4 da cavidade do forno do Exemplo 13.3, se todo o forno receber um fluxo térmico uniforme correspondente a uma potência total de 1522 W.

Passo 1

Vamooos que vamooos!!

Bom, galera o exemplo 13.3 nos deu o seguinte esquema:

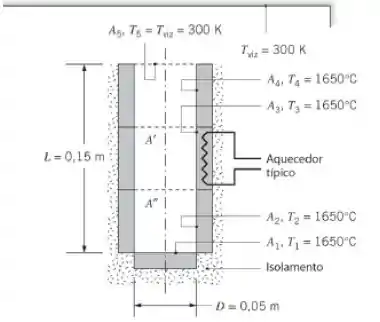
A questão nos pede para determinar as temperaturas das superfícies de 1 a 4 da cavidade do forno, não é?

Usando as equações que o exemplo já nos deu:

q = A 1 F 15 σ T 1 4 - T 5 4         ∴         q " = F 15 σ T 1 4 - T 5 4                     ( 1 )

q = A 2 F 25 σ T 2 4 - T 5 4         ∴         q " = F 25 σ T 2 4 - T 5 4                     ( 2 )

q = A 3 F 35 σ T 3 4 - T 5 4         ∴         q " = F 35 σ T 3 4 - T 5 4                     ( 3 )

q = A 4 F 45 σ T 4 4 - T 5 4         ∴         q " = F 45 σ T 4 4 - T 5 4                     ( 4 )

Nós temos que:

T 5 = T v i z = 1000   K

σ = 5,67 × 10 - 8 W m 2 K 4

O fluxo de calor perdido por área nós conseguimos calcular:

q " = q A t  

Sabemos que:

q = 1522   W

A t = π D 2 4 + π D L = π 0,05 2 4 + π 0,05 0,15  

Então:

q = 1522   W π 0,05 2 4 + π 0,05 0,15   = 59626,8 W m 2    

Então a única coisa que nos falta é achar os fatores de forma, certo?

Passo 2

O exemplo 13.3 nos deu:

F 51 = 0,0263

F 52 = 0,0294

F 53 = 0,1163

F 54 = 0,828

Usando a reciprocidade para achar o que realmente precisamos:

F 15 = A 5 A 1 F 51         ∴       F 15 = F 51 = 0,0263

F 25 = A 5 A 2 F 5 2         ∴       F 25 = π 0,05 2 4 π 0,05 0,15   3 0,0294 = 0,0073

F 3 5 = A 5 A 3 F 5 3         ∴       F 3 5 = π 0,05 2 4 π 0,05 0,15   3 0,1163 = 0,0 291

F 4 5 = A 5 A 4 F 5 4         ∴       F 4 5 = π 0,05 2 4 π 0,05 0,15   3 0,828 = 0 , 207

Agora vamos substituir:

  59626,8 = ( 0,0263 ) ( 5,67 × 10 - 8 ) T 1 4 - 300 4                     ( 1 )

  59626,8 = ( 0,0073 ) ( 5,67 × 10 - 8 ) T 2 4 - 300 4                     ( 2 )

59626,8 = ( 0,0291 ) ( 5,67 × 10 - 8 ) T 3 4 - 300 4                     ( 3 )

  59626,8 = ( 0,207 ) ( 5,67 × 10 - 8 ) T 4 4 - 300 4                     ( 4 )

Resolvendo as quatro equações simultaneamente utilizando um software:

T 1 = 2515   K

T 2 = 3459   K

T 3 = 2452   K

T 4 = 1502   K

Shooow !! Chegamos ao fim de mais umaaa !!

Resposta

T 1 = 2515   K

T 2 = 3459   K

T 3 = 2452   K

T 4 = 1502   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma janela de vidro duplo. A superfície do vidro pode ser tratada com um revestimento de baixa emissividade para reduzir sua emissividade de ε = 0,95 para ε = 0,05 . Determine o fluxo térmic
A configuração mostrada é usada para calibrar um medidor de fluxo térmico. O medidor tem uma superfície negra com 8m m de diâmetro, que é mantida a 1 7 ° C por uma placa de suporte resfriada com água.
Considere discos negros, paralelos e coaxiais, separados por uma distância de 0,20m . O disco inferior, com diâmetro de 0 , 2 0m , é mantido a 500K , enquanto a vizinhança está a 3 1 0K .Qual será a t
Uma cavidade cilíndrica com diâmetro D e profundidade L é usinada em um bloco de metal, e as condições são tais que as suas superfícies da base e lateral são mantidas a T 1=95 0K e T 2 = 65 0K , respe
Considere as seguintes fendas, cada uma com largura W , que foram usinadas em um bloco de material sólido.(a) Para cada caso, obtenha uma expressão para o fator de forma da fenda com relação à vizinha