Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 128
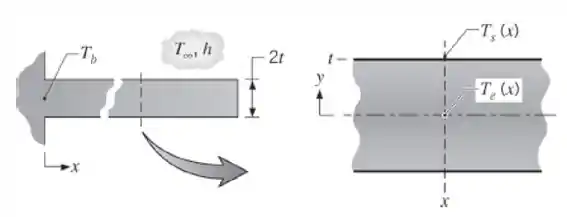
Considere uma superfície estendida de seção transversal retangular com transferência de calor na direção longitudinal. Nesse problema procuramos determinar condições nas quais a diferença de temperaturas transversal (direção y) no interior da superfície estendida é desprezível em comparação com a diferença de temperaturas entre a superfície e o ambiente, de tal forma que a análise unidimensional da Seção 3.6.1 seja válida.
- Suponha que a diferença de temperaturas transversal seja parabólica e com a forma:
- Escreva uma expressão para o fluxo térmico convectivo na superfície, na posição x. Igualando as duas expressões para o fluxo térmico condutivo e para o convectivo, identifique o parâmetro que determina a razão .
- Com base na análise anterior, desenvolva um critério para estabelecer a validade da hipótese unidimensional usada para modelar uma superfície estendida.
na qual é a temperatura da superfície e é a temperatura na linha central em cada ponto x. Usando a lei de Fourier, escreva uma expressão para o fluxo térmico condutivo na superfície, , em termos de e .
Passo 1
Vamos com tudo galerinha ??
Antes de qualquer coisa vamos ver de perto como vai ocorrer a transferência de calor na direção y:
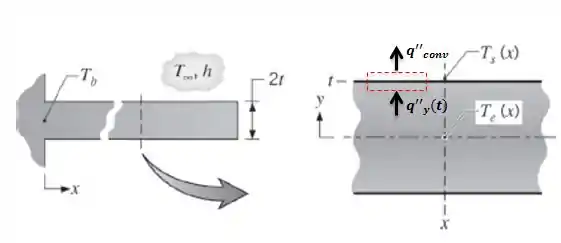
Na superfície nós teremos um volume diferencia que está recendo calor do seu interior e perdendo calor por convecção para o exterior, certo?
Como dito na letra (a) teremos uma distribuição parabólica de temperatura:
Isolando
E agora só precisamos achar em termos de e , ok?
Se é uma transferência de calor por condução:
Derivando a equação da temperatura em função de y:
Substituindo e :
Achamos nossa letra (a) !!
Passo 2
Na letra (b) nós queremos achar uma expressão para o fluxo térmico convectivo na superfície, na posição x, ok?
O calor convectivo nós já estamos carecas de saber, não é?
Fazendo o balanço de massa quando nós teremos que:
Substituindo:
Como precisamos achar a razão :
Se nós reorganizarmos isso:
Lembrando que:
Então:
Se a razão entre as resistências é conhecida como número de Biot:
Portanto a razão entre as temperaturas é determinada pelo número de Biot, legal, não foi?
Passo 3
Na letra (c) o que nós queremos?
Desenvolva um critério para estabelecer a validade da hipótese unidimensional usada para modelar uma superfície estendida, não é?!
De acordo com que acabamos de ver podemos deduzir que a diferença de temperatura transversal será desprezível em comparação com se nós tivermos um número .
E quando nós temos estes valore s de Biot podemos dizer que a transferência de calor longitudinal predomina com relação a transferência de calor transversal, que será portanto negligenciado !!
Por isso, nós usaremos este critério para validar a hipótese unidimensional usada !
E fiiiim !!
Resposta
- ;