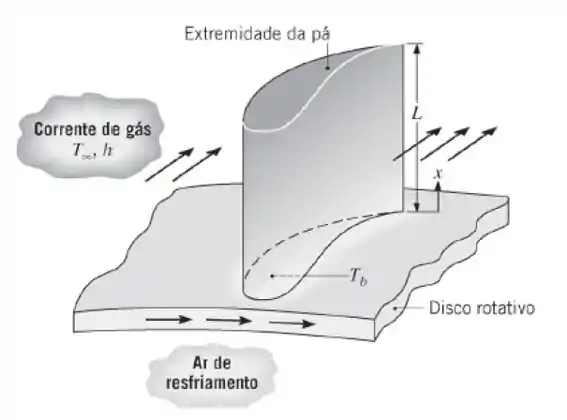
Pás de turbina montadas sobre um disco rotativo em um motor de turbina a gás estão expostas a uma corrente de gás a , que mantém um coeficiente de transferência de calor sobre a pá de . As pás, fabricadas em Inconel, , têm um comprimento . O perfil da pá possui uma área de seção transversal uniforme e um perímetro . Um sistema proposto para o resfriamento das pás, que envolve a passagem de ar através do disco de suporte, é capaz de manter a base de cada pá a uma temperatura de .

1. Sendo a temperatura máxima permissível para a pá de 1050°C e a extremidade da pá podendo ser considerada adiabática, o sistema de resfriamento proposto é satisfatório?
2. Para o sistema de resfriamento proposto, qual é a taxa na qual o calor é transferido de cada pá para o ar de resfriamento?

Vamos com tudo galerinha ??

Antes de qualquer coisa, como a pá possui uma extremidade adiabática, vamos olhar a Tabela 3.4 e ver o que ela nos diz:

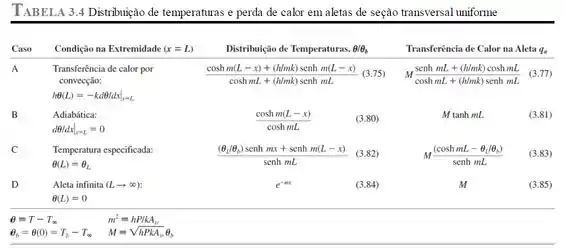
Como a temperatura máxima se dará quando , então a distribuição da temperatura será:

Lembrando que:

E sabendo que:

Substituindo:

Como a temperatura máxima permissível para a pá de 1050°C o sistema de resfriamento é adequado !!