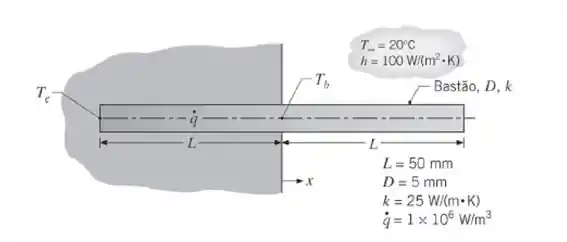
Um bastão de metal de comprimento 2L, diâmetro D e condutividade térmica k está encravado em uma parede de um isolante perfeito, expondo a metade do seu comprimento a uma corrente de ar que se encontra a temperatura e fornece um coeficiente convectivo h na superfície do bastão. Um campo eletromagnético induz uma geração de energia volumétrica a uma taxa uniforme no interior da porção encravada do bastão.
- Deduza uma expressão para a temperatura na base da metade exposta do bastão, em regime estacionário. A região exposta pode ser aproximada como uma aleta muito longa.
- Deduza uma expressão para a temperatura na extremidade da metade encravada do bastão, em regime estacionário.
- Usando valores numéricos fornecidos no esquema, represente graficamente a distribuição de temperaturas no bastão e descreva características importantes desta distribuição. O bastão se comporta como uma aleta muito longa?
Passo 1
Eu sei que vocês estão cansados, mas respirem fundo e vamos seguindo !!
Como nós temos uma taxa uniforme de calor sendo transmitido para aleta:
Se considerarmos que ela se comporta como aleta infinita, podemos olhar na Tabela 3.4:
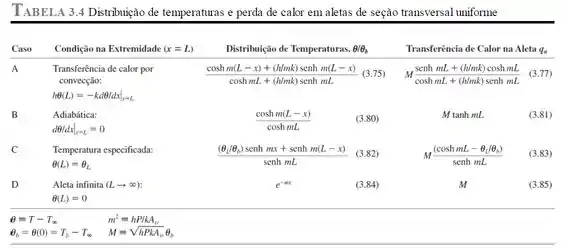
Sendo assim:
Substituindo
A taxa de transferência também pode ser escrita como:
Substituindo:
Passo 2
Na letra (b) nós precisamos achar a temperatura na base . Como estamos falando da parte isolada e teremos uma transferência de calor unidimensional e uniforme.
Usando a distribuição da temperatura para estes casos, dado pelo livro laaaa na Equação 3.47:
A temperatura quando :
Já finalizamos mais uma letra e bora continuar !!
Passo 3
Na letra (c) nós temos que:
Calculando com ajuda do Passo 1:
Substituindo:
Em graus Celsius:
Agora podemos achar usando a fórmula do Passo 2:
Em graus Celsius:
Já obtemos os valores, certo?
Agora precisamos plotar no gráfico, mas como?
Vamos analisar, na parte isolada a temperatura terá uma função parabólica, como vimos no Passo 2.
De acordo com a Tabela 3.4 a distribuição da temperatura para o intervalo é exponencial.
Se já sabemos como as duas funções se comportam podemos ter uma ideia de como o gráfico ficaria, mas lançando os dados no Excel, por exemplo, podemos ver melhor:
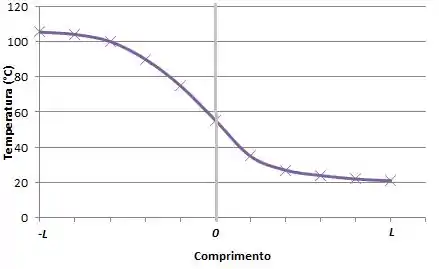
E fechamos mais uma com chave de ouro !!
Resposta
- ;