Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 68

A transmissividade espectral de um filme de polímero com 50   μ m de espessura é medida no intervalo de comprimentos de onda 2,5   μ m   ≤   λ   ≤   15   μ m . A distribuição espectral pode ser aproximada por τ λ   =   0,80 para 2,5   μ m   ≤   λ   ≤   7   μ m , τ λ   =   0,05 para 7   μ m , λ   ≤   13   μ m e τ λ   =   0,55 para 13   μ m ,   λ   ≤   15   μ m . Dados de transmissividades fora do intervalo não podem ser obtidos devido às limitações associadas à instrumentação. Um engenheiro deseja determinar a transmissividade total do filme.

(a) Estime a transmissividade total máxima possível do filme associada à irradiação de um corpo negro a T   =   30 ° C .

(b) Estime a transmissividade total mínima possível do filme associada à irradiação de um corpo negro a T   =   30 ° C .

(c) Repita as partes (a) e (b) para um corpo negro a T   =   600 ° C .

Passo 1

Vamos lá!! antes de mais nada precisamos fazer nossas famosas considerações. Hehe (u.u)

I - S u p e r f i c i e   s e   c o m p o r t a   c o m o   u m   c o r p o   n e g r o

Agora vamos fazer um esqueminha do que acontece junto com nosso gráfico espectral!

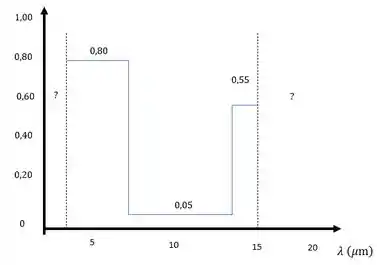
Passo 2

(a)

A transmissividade máxima total é dada para τ λ , 1 = τ λ , 5 = 1

τ = ∫ 0 ∞ τ λ E λ ,   b T d λ E b T

τ λ , 1 ∫ 0 λ 1 E λ ,   b T d λ E b T + τ λ , 2 ∫ λ 1 λ 2 E λ ,   b T d λ E b T + τ λ , 3 ∫ λ 2 λ 3 E λ ,   b T d λ E b T + τ λ , 4 ∫ λ 3 λ 4 E λ ,   b T d λ E b T + τ λ , 5 ∫ λ 4 λ 5 E λ ,   b T d λ E b T

τ = τ λ , 1 F 0 - λ 1 + τ λ , 2 F λ 1 - λ 2 + τ λ , 3 F λ 2 - λ 3 + τ λ , 4 F λ 3 - λ 4 + τ λ , 5 F λ 4 - ∞

Onde T s = 303 K , assim temos:

F 0 - λ 1 = 1,26 ⋅ 10 - 5

F λ 1 - λ 2 = 0,08738

F λ 2 - λ 3 = 0,3820

F λ 3 - λ 4 = 0,1015

F λ 4 - ∞ = 0,4291

Assim:

τ m a x = 1 ⋅ 1,26 ⋅ 10 - 5 + 0,8 ⋅ 0,08738 + 0,05 ⋅ 0,3820 + 0,55 ⋅ 0,1015 + 1 ⋅ 0,4291

τ m a x 303   K = 0,574

Passo 3

(b)

Precisamos somente repetir o passo 1 para τ λ , 1 = τ λ , 5 = 0

Assim temos:

τ m i n = 0 + 0,8 ⋅ 0,08738 + 0,05 ⋅ 0,3820 + 0,55 ⋅ 0,1015 + 0

τ m i n 30 3   K = 0,145

Passo 4

(c)

Repetindo o passo 2 e 3 para T = 873   K temos:

F 0 - λ 1 = 0,7469

F λ 1 - λ 2 = 0,6490

F λ 2 - λ 3 = 0 , 1906

F λ 3 - λ 4 = 0,01 84

F λ 4 - ∞ = 0 , 0 4 4 1

Assim:

τ m a x = 1 ⋅ 0,7469 + 0,8 ⋅ 0,6490 + 0,05 ⋅ 0,1906 + 0,55 ⋅ 0,0184 + 1 ⋅ 0,0441

τ m a x 6 00   K = 0 , 681

τ m i n = 0 + 0,8 ⋅ 0,6490 + 0,05 ⋅ 0,1906 + 0,55 ⋅ 0,0184 + 0

τ m i n 6 00   K = 0 , 539

Isso é tudo pessoal! \o/

Resposta

τ m a x 303   K = 0,574

τ m i n 303   K = 0,145

τ m a x 600   K = 0,681

τ m i n 600   K = 0,539

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa opaca horizontal é bem isolada nas bordas e na superfície inferior. A irradiação da placa é 3.000 W/m2, das quais 500 W/m2 é refletida. A placa tem temperatura uniforme de 700 K e poder emis
Um forno com janela de vidro de 40 cm x 40 cm pode ser aproximado como um corpo negro a 1.200 K. Considerando que a transmissividade do vidro é 0,7 para radiação em comprimentos de onda inferiores a 3
Considere uma placa opaca horizontal bem isolada nas bordas e na superfície inferior. A placa é mantida a 500 K, tem absortividade hemisférica total de 0,51 e a seguinte função de emissividade espectr
Uma placa horizontal está passando por uma irradiação uniforme nas superfícies superior e inferior. A temperatura do ar ambiente em torno da placa é 290 K, com coeficiente de transferência de calor po
A variação da absortividade espectral de uma superfície é dada na figura a seguir. Determine a absortividade e a refletividade média da superfície para uma radiação originária de uma fonte a T = 2.500