Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 101

Como as fórmulas para escoamento compressível em duto se compartam para quedas de pressão pequenas? Admita que o ar a 20°C entre em um tubo de 1 cm de diâmetro e 3 m de comprimento. Se   f - = 0,028 com p 1 = 102   k P a e p 2 = 100   k P a , calcule a vazão em massa em kg/h para (a) escoamento isotérmico, (b) escoamento adiabático e (c) escoamento incompressível com a massa específica de entrada.

Passo 1

Vamos lá galerinha, nas 3 letras temos que calcular vazão mássica, certo? Então precisamos a densidade dos fluidos, das áreas transversais de escoamento e das velocidades!!

Pra começar, vamos fazer uma análise rápida!!! Bem, note que há uma diferença de apenas 2% na pressão do ponto 1 do ponto 2. Outra coisa é que temos já que o nosso f   L D = 0,028 3 0,01 = 8,4 será igual para geral.

(a) Por sua vez, para a seção 1, temos temperatura e pressão...Opa, então já podemos calcular qual é a densidade do ar nesse ponto!!

ρ 1 = p R T

Onde esse R aí a gente tira da tabela A.2 do livro para o ar atmosférico.

ρ 1 = 102000 287 273 + 20 = 1,213   k g / m ³

Passo 2

Para um sistema isotérmico, temos que:

m ˙ A 2 = p 1 2 - p 2 2 R T f L D + 2 ln ⁡ p 1 p 2 = 102000 2 - 100000 2 287 293 8,4 + 2 ln ⁡ 102 100 = 569

Então com isso conseguimos descobrir facilmente qual deve ser o valor da vazão mássica:

m ˙ A = 23,9

m ˙ = 23,9   π 4 0,01 2 = 0,00187   k g / s

Passo 3

(b) Para um sistema adiabático, temos que:

T 0 = 293   K

a 0 = k R T 0

Com os valores usuais do ar de 1,68 para k e R = 208   m 2 / s ² K , temos que:

a 0 = 343   m / s

Usando as equações 9.74 e 9.75 do livro, temos esse sistema aqui ó:

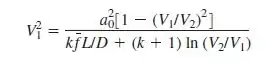
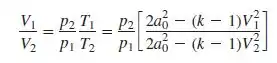
Note que temos um sistema, onde temos que chutar um valor de V 1 e V 2 , comece chutando dizendo que as velocidades são iguais, ou seja, V 1 V 2 = 1 e faça o processo de convergência. Você vai ver ao final que o valor de convergência será bem próximo de 1, pois converge quando V 1 V 2 = 0,9803 .

V 1 2 = 343 2 1 - 0,9803 2 1,4 8,4 + 2,4 ln ⁡ 1,02 = 388 → V 1 = 19,7 m s

Portanto, temos que a vazão mássica será dada por:

m ˙ = ρ 1 A V 1 = 1,223   π 4 0,01 2 19,7 = 0,00188   k / s

Passo 4

(c) Para um sistema incompressível:

Δ p = f L D ρ 2 V 2

2000 = 8,4 1,213 2 V 2 → V = 19,8   m / s

Portanto, temos que a vazão mássica será dada por:

m ˙ = ρ 1 A V 1 = 1,223   π 4 0,01 2 19 , 8 = 0,0018 9   k / s

Resposta

a m ˙ = 0,00187   k g / s

b m ˙ = 0,00188   k g / s

c m ˙ = 0,00188   k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jato de ar é soprado de um bocal perpendicularmente contra uma parede na qual existem duas tomadas de pressão. Um manômetro conectado à tomada colocada diretamente na frente do jato mostra uma altu
Considere um escoamento em regime permanente, incompressível e sem atrito sobre a asa de um aeroplano voando a 200 km/h. O ar que se aproxima da asa está a 65 kPa (manométrica) e -10°C. Em certo ponto
Uma corrente de líquido movendo a baixa velocidade sai de um bocal apontado diretamente para baixo. A velocidade pode ser considerada uniforme na seção de saída do bocal e os efeitos de atrito podem s
Água escoa de um tanque muito grande através de um tubo de 5 cm de diâmetro. O líquido escuro no manômetro é mercúrio. Estime a velocidade no tubo e a vazão de descarga. (Considere o escoamento sem at
Um barômetro de mercúrio é transportado em um carro em um dia em que não há vento e a temperatura do ar é 20°C. A leitura correta do barômetro é 761 mm de mercúrio. Uma janela é ligeiramente aberta qu