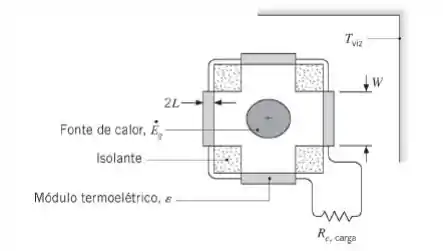
O gerador de potência elétrica de um satélite em órbita é composto por uma fonte de calor cilíndrica e longa, feita de urânio, que se encontra no interior de um recipiente de seção transversal quadrada. A única forma do calor gerado pelo urânio deixar o recipiente é através de quatro filas de módulos termoelétricos do Exemplo 3.13. Os módulos termoelétricos geram potência elétrica e também emitem radiação para o espaço, caracterizado por . Considere a situação na qual há 20 módulos em cada fila, ou seja, um total de módulos. Os módulos estão ligados em série com uma carga elétrica de e tem uma emissividade de . Determine a potência elétrica gerada para , e . Também determine as temperaturas superficiais dos módulos para as três taxas de geração de energia térmica.

Agora vamos encontrar quem é o nosso :

O também é uma função de , então vamos substituí-lo:

Se a nossa energia produzida é igual a nossa energia dissipada, vamos ter que:

E ainda está faltando o nosso , não podemos esquecer dele! Podemos encontrar ele por essa equação aqui olha só:

Vamos começar com o nosso , ok?

Para o nosso , o será:

E por último, para o nosso , o será:

Nós temos três valores de , então vamos ter três valores diferentes de e de e de , certo?

Agora podemos montar o que achamos em um sistema de três equações e três incógnitas, começando pelo primeiro valor de , olha só:

Sistema a gente já está acostumado a resolver, né? Apesar deste ser mais complexo, a gente consegue tranquilo… E resolvendo esse carinha aí vamos ter que:

Agora é só retornar lá na nossa equação da potência:

Agora vamos para o segundo valor de , repetindo o mesmo procedimento…

Montar o sisteminha:

Resolvendo vamos ter que:

E usando a equação da potência:

E pra fechar…

Vamos para o terceiro valor de , repetindo o mesmo processo…

Montar o sisteminha:

Resolvendo teremos:

E usando a equação da potência:

Uhull! Conseguimos!