Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 109
Considere um tubo em preenchido com mercúrio, exceto por de altura na parte superior, como mostra a Figura . O diâmetro do braço direito do tubo em é e o diâmetro do braço esquerdo é o dobro disso. Óleo com gravidade específica de é despejado no braço esquerdo, forçando parte do mercúrio do braço esquerdo a passar para o direito. Determine a quantidade máxima de óleo que pode ser adicionada ao braço esquerdo.
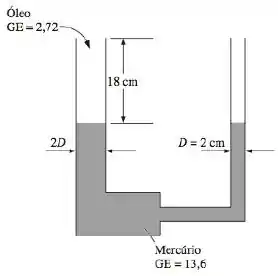
Passo 1
Antes de tudo vamos assumir e enunciar algumas propriedades, assumindo que os dois líquidos são incompressíveis e que o tubo em é perfeitamente vertical.
Temos a gravidade específica do óleo e para o mercúrio.
Para determinarmos a quantidade de volume de óleo máxima, temos que calcular o quão o mercúrio ira se deslocar com o despejar do óleo.
Inicial o nível de mercúrio nos dois braços são iguais, após o despejo do óleo no braço esquerdo, isto vai fazer com que nível de mercúrio no braço direito aumente e nível de mercúrio no braço esquerdo diminua. Note que a mesma quantidade que diminui o nível de mercúrio no braço esquerdo irá aumentar no braço direito. Portanto, se uma nível de mercúrio diminuir no braço esquerdo ira aumentar um nível no direito, mas note que o diâmetro dos braços são diferentes, e terão o mesmo volume de Mercúrio, logo o nível de um braço será maior que outro.
Passo 2
Seguindo oque foi dito nos passo 1, temos:
Verificando isto:
Isolando e simplificando:
Agora, podemos determinar calculando a equivalência de pressões em cada braço, escolhendo um ponto equivalente na horizontal e temos:
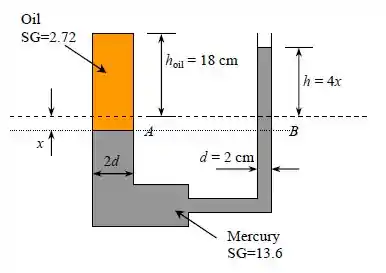
Isolando , temos:
Passo 3
Agora que temos o deslocamento da coluna, quando foi despejado óleo, podemos calcular o volume máximo que foi despejado para este deslocamento.