Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 1.Problemas - Ex. 93

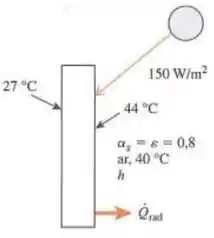
As superfícies interna e externa de uma parede de 25 cm de espessura no verão estão a 27°C e 44°C, respectivamente. A superfície externa da parede troca calor por radiação com as superfícies vizinhas a 40°C e também por convecção com ar ambiente a 40°C com um coeficiente de transferência de calor por convecção de 8 W m 2 K . A radiação solar incide na superfície a uma taxa de 150   W / m 2 . Se a emissividade e a absortividade da superfície externa forem 0,8, determine a condutividade térmica efetiva da parede.

Passo 1

Vamos para mais uma beeeem legal, animadíssimos?

Então bora começar!

Nós precisamos saber quais energias estão sendo transferidas, certo?

A parede externa absorve a energia que esta sendo emitida pelo sol, energia convectiva e a radiação, toda esta energia é conduzida para a parede interior por condução, não é?

Sendo assim:

q c o n d ˙ = q c o n v ˙ + q r a d ˙ + q s o l a r ˙

Vamos começar vendo como calculamos cada uma:

q c o n d ˙ = k T 2 - T 1 L

q c o n v ˙ = h T 0 - T 2

q r a d ˙ = ε σ T 0 4 - T 2 4

q s o l a r ˙ = α s I

Aqui nós estamos chamando T 1 da temperatura interna da parede, T 2 a temperatura externa da parede, T 0 temperatura do ar.

O que nós sabemos?

T 1 = 27 ° C + 273 = 30 0   K

T 2 = 44 ° C + 273 = 3 17   K

T 0 = 40 ° C + 273 = 3 13   K

L = 25   c m = 0,25   m

h = 8 W m 2 K

ε = α s = 0,8

I = 150 W m 2

Tabelado nós temos a constante de Boltzmann:

σ = 5,67 × 10 - 8

Olhem só!! A questão parecia assustador mas tudo que precisamos, nós temos !! Então bora substituir nesta nova equação:

k T 2 - T 1 L = h T 0 - T 2 + ε σ T 0 4 - T 2 4 + α s I

Então:

k 317   K - 300 K 0,25   m = 8 W m 2 K 313   K - 317   K + 0,8 5,67 × 10 - 8 313   K 4 - 3 17   K 4 + 0,8 150 W m 2

k = 0,9605 W m . ° C

Portanto, a condutividade térmica deve ser igual a 0,9605 W m . ° C !!

Gostaram?

Resposta

0,9605 W m . ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

74 - A maioria da energia que consumimos como alimento é convertida em energia térmica nos processos vinculados a todas nossas funções corporais e é, ao final, perdida como calor do corpo para o ambie
80 - Seja o tubo de vapor d’água do Exemplo 1.2. O gestor de utilidades quer uma recomendação sua sobre métodos para reduzir a perda térmica para a sala e propõe duas opções. A primeira opção restring
70 - Um computador é constituído por um conjunto de cinco placas de circuitos integrados (PCI), cada uma dissipando P p = 20W de potência. O resfriamento dos componentes eletrônicos de uma placa é via
73 - Considere as condições do Problema 1.22, porém a temperatura da vizinhança é de 25℃ ℃ e a troca térmica por radiação com a vizinhança não é desprezível. Sendo o coeficiente convectivo igual a 6,4
66 - Uma chapa vertical de metal de Woods está presa a um substrato por uma superfície e é fundida ao ser irradiada uniformemente por uma fonte de laser sobre a superfície oposta. O metal encontra-se