Considere o ventilador e os dados de desempenho do Problema 10.84. Para , a pressão dinâmica é equivalente a 4 mm de coluna de água. Avalie a área de saída do ventilador. Trace um gráfico do aumento de pressão total e da potência de entrada (em hp) versus vazão em volume. Calcule a eficiência total do ventilador e mostre a curva no gráfico. Determine o ponto de melhor eficiência e especifique os valores de operação do ventilador neste ponto.

Passo 1
Tá legal, vamos começar o exercício escrevendo a equação da eficiência estática do ventilador, dada pela razão entre a potência hidráulica produzida e a potência mecânica que é fornecida ao sistema, ou seja:
E, sabemos que a potência hidráulica é dada por:
Em que é a queda de pressão total, que pode ser escrita como:
Agora, vamos escrever a equação para a pressão dinâmica:
E, dessa forma, a altura correspondente a pressão dinâmica pode ser escrita como:
Substituindo a expressão para :
Passo 2
Então, através da fórmula da vazão, temos:
Substituindo a expressão encontrada para no passo 1, temos:
Substituindo os valores conhecidos, temos:
Passo 3
Tá legal, agora para desenhar os gráficos do aumento da pressão total e da potência de entrada versus a vazão, precisamos dessas expressões em função da vazão, então, conforme vimos no passo 1, o aumento de pressão total será:
Só que é a queda de altura total, soma da queda estática e dinâmica, dada por:
Os valores para foram fornecidos no enunciado em função de e nós encontramos a expressão para , então, temos:
E, substituindo a velocidade em função da vazão, temos:
Substituindo essa expressão na equação da queda de pressão, temos:
Então, plotando essa equação com os valores conhecidos e tabelados no enunciado, temos:
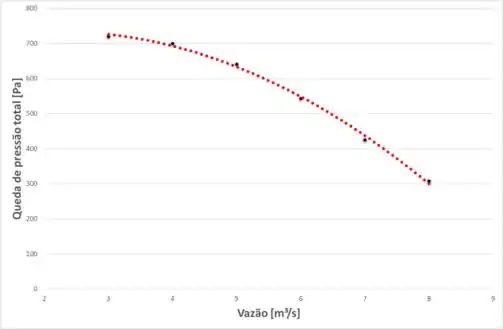
Passo 4
Agora para o gráfico da potência de entrada versus a vazão, basta plotar os resultados tabelados fornecidos no enunciado, então, temos:
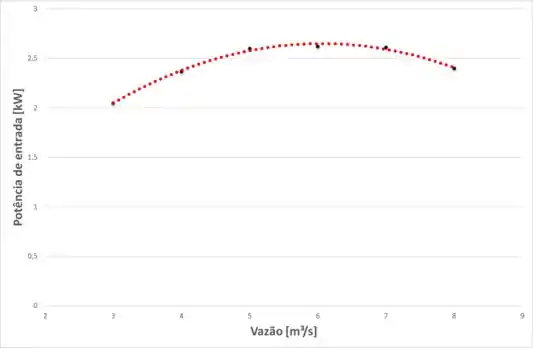
Passo 5
Para a curva de eficiência, vamos voltar à equação da eficiência do passo 1:
E sabemos que a potência hidráulica é dada por:
Então, substituindo a expressão encontrada para no passo 3, temos:
Então a equação da eficiência se torna:
E o gráfico dessa curva será:
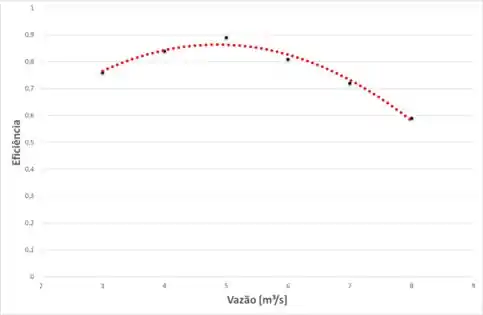
O ponto de melhor eficiência será para . Nesse ponto, temos:
No gráfico da queda de pressão do passo 3, para essa vazão, temos uma queda total de:
E, então, a equação da eficiência se torna: