Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 60
Ao contrário do que se possa esperar, uma esfera de aço sólida pode flutuar na água devido ao efeito da tensão superficial. Determine o diâmetro máximo de uma esfera de aço que flutuaria em água a . Qual seria sua resposta para uma esfera de alumínio? Suponha que as densidades das esferas de aço e de alumínio sejam, respectivamente, e .
Passo 1
O exercício quer que a gente calcule o diâmetro máximo que uma esfera pode ter para flutuar. O enunciado também diz que a esfera é sustentada pelo efeito da tensão superficial. Ou seja, a força gerada pela tensão superficial equilibra o peso da esfera para ela não afundar e ficar parada boiando. Por conta disso, essas duas forças opostas devem ser iguais.
Além disso, para a esfera ter o maior diâmetro possível, é necessário que a força da tensão superficial dê o máximo de sustentação à esfera! Para isso, o ângulo de contato entre a superfície da esfera e a superfície da água deve ter . Dessa forma, a força fica vertical para cima. A ága precisa estar em contato com o meio da esfera para ter um maior comprimento de contato. A figura abaixo mostra isso!
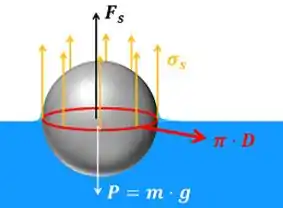
onde é a massa da esfera e é a aceleração da gravidade.
Passo 2
Para calcular quanto vale a força , temos que lembrar que a tensão superficial é a força superficial dividida pelo comprimento de contato entre a superfície líquida e a superfície sólida. Além disso, temos que lembrar que esse comprimento precisa ser igual ao perímetro da esfera.
O peso da esfera é a multiplicação entre o volume da esfera, a densidade da esfera e a aceleração da gravidade .
Substituindo essas fórmulas na equação das forças, encontramos:
Passo 3
A tensão superficial da água a se encontra na tabela do livro.
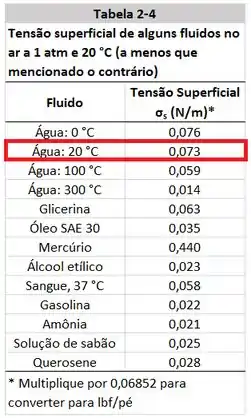
No próximo passo nós vamos iniciar as contas.
Passo 4
Se a esfera for de aço, é igual a:
Se a esfera for de alumínio, é igual a: