Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 108

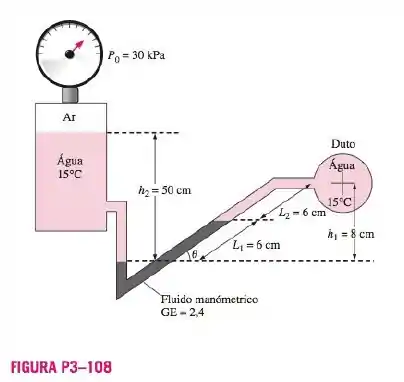
A pressão da água escoando através de um tudo é medida pelo dispositivo mostrado na Figura P 3 - 108 . Para os valores dados, calcule a pressão no duto.

Passo 1

Primeiro de tudo, neste exercício temos que considerar algumas coisas como:

Todos os líquidos são incompressíveis, o efeito da coluna de ar na pressão será irrelevante.

Assumindo isto temos algumas propriedades para enunciar:

Temos que a densidade da água será a padrão de ρ w = 1000   k g / m 3 , e aproveitando irei tomara notação de w para qualquer coisa referente a água ou seja h w seria altura da coluna de água, certo?

Tendo estes itens explanados, temos que para resolver está questão iremos começar com a pressão indicada no manômetro, e iremos movendo ao longo dos tubos (somando as pressões assim como vamos “andado” para baixo), diminuindo a pressão (assim como vamos para cima nos tubos).

Passo 2

Executando oque foi dito no passo 1, temos:

P 0 + ρ w g h w 1 - ρ G E g h G E - ρ w g h w 2 = P d u t o

Arruando a equação e vamos enunciar as colunas dos fluidos:

P d u t o = P 0 + ρ w g h w 1 - ρ G E g h G E - ρ w g h w 2

P d u t o = P 0 + ρ w g h w 1 - ρ G E h G E - h w 2

Temos que a coluna de fluido manométrico e a outra coluna de água do duto precisam ser calculados com um pouco de trigonometria.

Temos um triangulo retângulo:

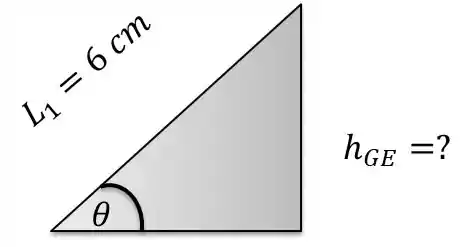
Como desejamos a coluna vertical de liquido, basta aplicarmos conceito de s e n :

s e n   θ = h G E L 1

h G E = s e n   θ   L 1

A mesma lógica se aplica a coluna de água h w 2 .

Você deve estar se perguntado, mas como saberemos o valor de θ , perceba que temos um outro triangulo retângulo que pode nós dar esta informação, este aqui:

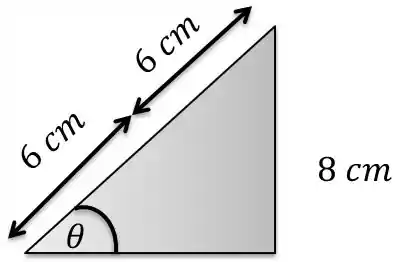
Portanto temos que:

s e n   θ = 8 6 + 6 = 0.6667

Passo 3

Agora que possuímos todas as variáveis, finalmente podemos aplicar na equação que montamos anteriormente e ter o resultado final:

P d u t o = P 0 + ρ w g h w 1 - ρ G E h G E - h w 2

P d u t o = 30 + 1000 ∙ 9.81 ∙ 0,5 - 2,4 ∙ 0 , 06 ∙ 0 , 6667 - 0 , 06 ∙ 0 , 6667

P d u t o = 33 ,   6   k P a

Resposta

P d u t o = 33 ,   6   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o Problema 3-126. Usando o EES (ou um outro aplicativo), investigue o efeito da aceleração sobre a inclinação da superfície livre da água do tanque. Faça a aceleração variar de 0m / s 2 at
É preciso projetar sapatos que permitam a pessoas com até 80 kg caminhar sobre água doce ou água do mar. Os sapatos devem ser feitos de plástico injetado na forma de uma esfera,uma bola de futebol ame
Um balão de ar elástico com diâmetro de 30 cm é acoplado à base de um contêiner parcialmente preenchido com água a + 4 ℃ ℃, como mostra a Figura. Se a pressão do aracima da água aumentar gradualmente
Reconsidere o Problema 3-128. Usando o EES (ou outro aplicativo), investigue o efeito da pressão do ar acima da água sobre a força no cabo. Faça a pressão variar de 0,1 MPa até 10 MPa. Represente graf
Um contêiner cilíndrico cujo peso é de 79 N é invertido e pressionado na água, como mostra a Figura. Determine a altura diferencial h do manômetro e a força F necessária paramanter o contêiner na posi